メービウスの帯（読み）メービウスノオビ（その他表記）Möbius' strip

デジタル大辞泉

メービウス‐の‐おび【メービウスの帯】

《Möbius strip》⇒メビウスの帯

出典　小学館

改訂新版　世界大百科事典

メービウスの帯 (メービウスのおび)
Möbius' strip

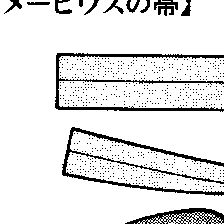
細長い長方形の紙を空間のなかで180°だけねじったのち，長方形の短い2辺を反対の向きに重なるようにはり合わせて一つの曲面をつくる（図）。いま，1匹のアリがこの曲面に沿って真ん中の線上をはっているとすれば，アリは一周したときには初めの側と反対の側にいて，初めとは逆の向きに立っている。このようなわけで，この曲面は表裏の区別のつけられない曲面（単側面）で，また，左まわりと右まわりの区別のつけられない曲面（向きのつけられない曲面）である。この曲面は，このような性質を初めて指摘したA.F.メービウスにちなんで〈メービウスの帯〉と呼ばれている。〈メービウスの帯〉については予想を誤りがちな次の現象が起こる。〈メービウスの帯〉を真ん中の線に沿って切ってもひと続きのままで，さらにその真ん中の線に沿って切ると二つに分離するが，それらは互いに絡みあっている。
→位相幾何学
執筆者：中岡 稔

図－メービウスの帯

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

メービウスの帯【メービウスのおび】

長方形の紙（テープ）を一度ねじって対辺をのりづけして得られる曲面（輪）。表裏の区別がない曲面の最も簡単な例。位相幾何学で研究される。テープ幅の中央を切っても輪はひと続きのままで２つの輪に分離しない。ドイツの数学者アウグスト・フェルディナント・メービウス〔1790-1868〕にちなむ。→位相幾何学

出典　株式会社平凡社

世界大百科事典（旧版）内のメービウスの帯の言及

【位相幾何学】より

…閉曲面からその上にあるいくつかの円板の内部を取りのぞくと縁のある曲面が作れるが，このような曲面と位相的性質を異にする縁のある曲面が，1858年にメービウスにより発見された。この曲面はテープを180度ひねって両端をはり合わせて作られる曲面でメービウスの帯Möbius stripと呼ばれる(図4-a)。メービウスの帯の縁は円と同相である。…

【位相幾何学】より

…閉曲面からその上にあるいくつかの円板の内部を取りのぞくと縁のある曲面が作れるが，このような曲面と位相的性質を異にする縁のある曲面が，1858年にメービウスにより発見された。この曲面はテープを180度ひねって両端をはり合わせて作られる曲面でメービウスの帯Möbius stripと呼ばれる(図4-a)。メービウスの帯の縁は円と同相である。…

※「メービウスの帯」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」