向き（読み）ムキ（英語表記）orientation

デジタル大辞泉

むき【向き】

１ 向いている方向・方角。「風の向き」「北向きの部屋」
２ 関心・希望などの向かう方面や傾向。また、それらの内容。「物事を楽観する向きがある」「願いの向きを伝える」
３ 人。おかた。「御希望の向きはおいでください」
４ 適していること。似つかわしいこと。「向き不向きを考えて仕事を割り振る」「学生向きの本」
５ （「むきになる」の形で）つまらないことでも本気になること。「向きになって怒る」
[類語]方位・方向・方角・方

出典　小学館

改訂新版　世界大百科事典

向き (むき)
orientation

われわれは直線，平面上の回転，空間におけるらせん形には二つの異なった向きがつけられることを感覚的に知っている。このことは直線，平面や空間に対し向きという概念が考えられることを示唆しているが，数学ではもっと一般に，n次元実ベクトル空間，とくにユークリッド空間に対して向きの概念を定義する。まず次の事実に注目しよう。1直線上に0でないベクトル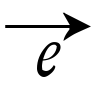があるとき，それはその直線上の向きを定め，このような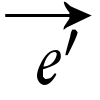，が二つあるとき，＝ae（a≠0）と書けるが，eとe′はa＞0ならば直線の同じ向きを定め，a＜0ならば異なる向きを定める（図）。平面上に一次独立な二つのベクトル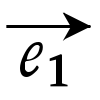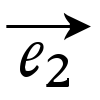，があるとき，これをこの順に並べたものを（，）で表せば，これは平面上の（回転の）向きを定め，このような（，）と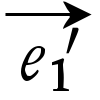（，）が二つあるとき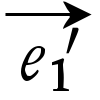，＝a₁₁＋a₁₂，＝a₂₁＋a₂₂（D＝a₁₁a₂₂－a₁₂a₂₁≠0）と書けるが，（，）と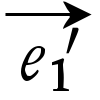（，）はD＞0ならば同じ向きを定め，D＜0ならば異なる向きを定める。これらの事実より抽象して，n次元実ベクトル空間Vの向きを次のように定義する。Vのn個の一次独立なベクトルをとり，それらを順序をつけて並べたものを順序づけられた基底という。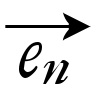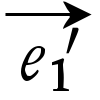（，，……，），（，，……，）を順序づけられた基底とするとき，

と書け，行列式D＝｜a_ij｜は0でない。いま，Vの順序づけられた基底全体の集合を考え，それに属する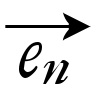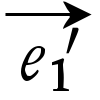（，，……，），（，，……，）はD＞0ならば同じクラスに入れ，D＜0ならば異なるクラスに入れる。このようにすればVの順序づけられた基底は二つのクラスに分かれるが，この各クラスをVの向きという。Vの向きを一つ指定したとき，Vに向きがつけられたといい，指定された向きを正の向き，他の向きを負の向きという。なお，多様体とくに曲面は局所的にはユークリッド空間だから，多様体の各点のまわりでは向きが指定できるが，これらが連続的に変わるように選べるとき，多様体に向きがつくという。多様体のなかには向きのつかないものもある。
執筆者：中岡 稔

図－向き

出典　株式会社平凡社「改訂新版　世界大百科事典」