リーマン多様体（読み）リーマンたようたい（その他表記）Riemannian manifold

改訂新版　世界大百科事典

リーマン多様体 (リーマンたようたい)
Riemannian manifold

微分可能多様体は局所的にみるかぎりユークリッド空間と考えられるので，ユークリッド空間のそれを利用して局所的な距離や角度を考えることは自然であろう。これは，地図のうえなどで現実によく行われることであり，したがってその考えの不都合さもよく知られているところである。すなわち，この距離があくまで局所的なものであるために，2点が離れているときは地図上の距離と実距離との差が大きくなってしまうのである。リーマン多様体とは，ひと口にいえば，このような不都合をなくすような距離を導入した微分可能多様体にほかならない。これをリーマン計量と呼ぶが，実際には，これは微分可能多様体の各点pの接ベクトル空間T_pにおいて〈距離のもと〉ともいうべき内積〈 ， 〉_pを考え，それを点pとともに少しずつ変えていくという操作によって行われる。数式を使っていうならば次のようである。まず点pのまわりの局所座標系（Xⁱ）をとる。これはT_pの自然な基底（e_i＝∂/∂Xⁱ）を定めるから，T_pの内積〈 ， 〉_pを与えるということは，この基底系に対して，対称正定値行列g_ij（X（p））＝〈e_i，e_j〉_pを与えるということと同じである。このとき，pのまわりに導入される座標系は一つとはかぎらないので，このような表現を使う場合には，別の座標系（Yⁱ）によっても同じ内積が定まることが要求される。これはYⁱの定める自然基底（ē_i＝∂/∂Yⁱ）がē_j＝Σ（∂Xⁱ/∂Y^j）e_iをみたすから，g_ij（X（p））およびg_ij（Y（p））が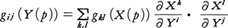，をみたすことであると翻訳される。このことはとりも直さず，g_ij（X（p））が二次共変テンソルであるということであり，したがって数学的にはリーマン多様体は，その計量として対称な正定値行列g_ij（X（p））を成分とする二次共変テンソルを与えた微分可能多様体であると定義される。なお，g_ij（X（p））の微分可能性は，もとの多様体の微分可能性に応じて要求されるが，少なくとも，連続性は必要とされるのが通常である。
執筆者：四方 義啓

出典　株式会社平凡社「改訂新版　世界大百科事典」