座標系（読み）ザヒョウケイ

デジタル大辞泉

ざひょう‐けい〔ザヘウ‐〕【座標系】

原点・座標軸など、座標をどう定めるかの基準を与えるもの。

出典　小学館

精選版 日本国語大辞典

ざひょう‐けいザヘウ‥【座標系】

1. 〘 名詞 〙 原点、座標軸など座標を定める仕組みのこと。直交座標系、斜交座標系、極座標系などがある。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

座標系
ざひょうけい

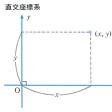
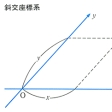
一般にある集合に対して、その各元に数量的なものを対応させて表す仕組みをこの集合における座標系といい、各元に対応する数量をその元の座標という。とくに幾何学においては幾何学的集合（直線、平面、空間、……、一般に多様体またはその部分集合）の元と数の組との間の一対一の対応を座標系という。幾何学的集合が与えられたとき、一つの基礎図形（座標軸など）を指定することによって座標系を導入することが多い。たとえば平面上では直交する2直線を、また、空間では互いに直交する3平面を基礎図形として直交座標系が導入される。より一般に平面上で交わる2直線を、また、空間では1点で交わる3平面を基礎図形とする座標系を斜交座標系という。「極座標」「円柱座標」についてはそれぞれの項目を参照されたい。平面または空間では直交座標または極座標が便利なことが多いが、斜交座標が有効な場合もある。

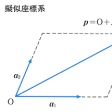
　擬似幾何学（アフィン幾何学）においては距離とか直交とかいう概念が意味をもたないから、いわゆる擬似座標系が用いられる。n次元アフィン空間Aⁿにおいて、任意の点Oと任意の一次独立なn個のベクトルa₁、a₂、……、a_nをとれば、Aⁿの任意な点pは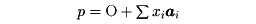

と表される。この(O ; a₁, a₂,……, a_n)をOを原点とする擬似座標系といい、(x₁, x₂,……, x_n)を点pの(O ; a₁, a₂,……, a_n)に関する擬似座標（または平行座標）という。

　n次元ユークリッド空間において直交座標(x₁, x₂,……, x_n)に対してn個のn変数関数
　　u_i＝u_i(x₁, x₂,……, x_n),
　　　i＝1, 2,……, n
が領域Dにおいて一対一かつ両連続であれば(u₁,u₂,……,u_n)はDの点と一対一に対応するからDにおける座標系とみなすことができる。これをDにおける曲線座標系という。このとき(n－1)個のu_iを固定して得られる曲線を座標曲線という。たとえば極座標(r,θ)は平面から原点を除いた領域における曲線座標系である。曲線座標系はユークリッド空間だけでなく、一般に多様体上の局所座標系として用いられる。一つの領域において二つの座標系が有効であれば、両者の間に一対一かつ両連続な関係が存在する。これを座標変換という。たとえば平面から原点を除いた領域において、直交座標(x, y)と極座標(r,θ)との間の座標変換は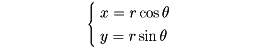

で与えられる。

［荻上紘一］

[参照項目] | 円柱座標 | 極座標

座標系（直交座標系）

座標系（斜交座標系）

座標系（擬似座標系）

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

座標系
ざひょうけい
coordinate system

直線や平面上，あるいは空間内の任意の点に座標を導入するための仕組みのこと。たとえば，直線 g 上に定点 O を定め，O を始点として長さの単位 OE をとると g の方向づけは自然に定まる。こうすると g 上には，任意の点Pに対して OP＝x・OE となる実数 x が定まるから，g 上の点全体と実数全体との間に，一対一の対応がつけられる。このときの対応を座標系といい，2点 O ，E によって g 上の座標系が定められるという。これを座標系 Ox などと書くことがある。同様にして，座標系 O－xy (平面) ，座標系 O－xyz (空間) などが使用される。直交座標系，斜交座標系，円柱座標系などがある。物理学では基準系を座標系と呼ぶことがある。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の座標系の言及

【座標】より

…直線，平面，空間における点に数または数の組を対応させて点の位置を表すしくみを座標系といい，点に対応する数または数の組をその点の座標という。座標を初めて考えたのはR.デカルトであり，彼はそれによって解析幾何学を創始し，幾何学的な図形を数の関係で表して幾何学を代数を用いて研究するという方法を開発したのである。…

※「座標系」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」