シンプソンの公式 (シンプソンのこうしき)
Simpson's rule
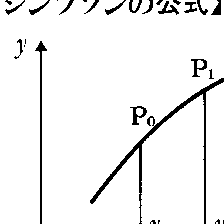
定積分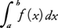 の近似計算のために次のようにして作られた公式である。区間[a,b]を2n等分した分点をa=x0,x1,x2,……,x2n=bとし,それらに対応するf(x)の値をy0,y1,y2,……,y2nとする。n個の小区間[x0,x2],[x2,x4],……,[x2n-2,x2n]において,関数y=f(x)を,それぞれ図におけるf(x)のグラフ上の3点{P0,P1,P2},{P2,P3,P4},……,{P2n-2,P2n-1,P2n}を通る放物線をグラフとする二次関数で置き換え,
の近似計算のために次のようにして作られた公式である。区間[a,b]を2n等分した分点をa=x0,x1,x2,……,x2n=bとし,それらに対応するf(x)の値をy0,y1,y2,……,y2nとする。n個の小区間[x0,x2],[x2,x4],……,[x2n-2,x2n]において,関数y=f(x)を,それぞれ図におけるf(x)のグラフ上の3点{P0,P1,P2},{P2,P3,P4},……,{P2n-2,P2n-1,P2n}を通る放物線をグラフとする二次関数で置き換え,
h=\(\frac{b-a}{2n}\)
とすると,各小区間における二次関数の積分の値はそれぞれ
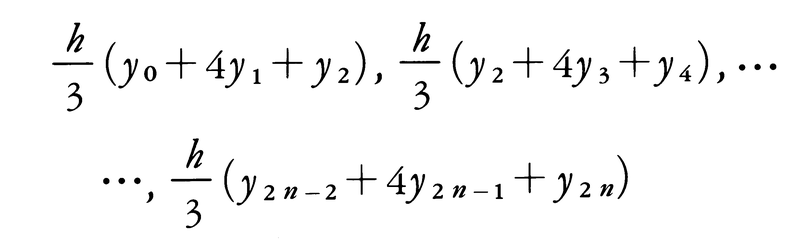
となるから,これらを加えて次の近似公式が得られる。これをシンプソンの公式という。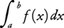
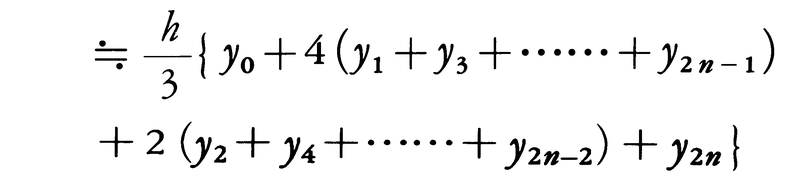
例えば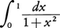 を計算するために,区間[0,1]を10等分すると,n=5,h=0.1,x0=0,x1=0.1,x2=0.2,……,x9=0.9,x10=1であり,対応するyの値から,
を計算するために,区間[0,1]を10等分すると,n=5,h=0.1,x0=0,x1=0.1,x2=0.2,……,x9=0.9,x10=1であり,対応するyの値から,
y0=1,y10=0.5
y1+y3+y5+y7+y9=3.931069
y2+y4+y6+y8=3.168657
となる。よってシンプソンの公式により,
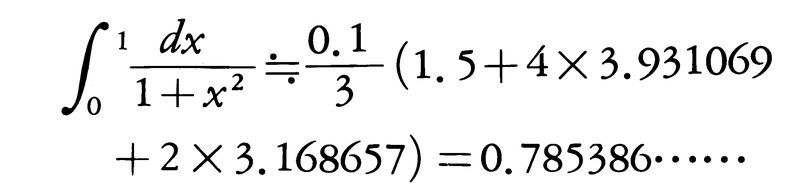
が得られる。なお,この定積分の正しい値はπ/4=0.785398……である。
執筆者:伊藤 清三
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
シンプソンの公式
シンプソンのこうしき
Simpson's rule
関数の数値積分に,実用上よく使われた公式で,イギリスの数学者 T.シンプソン(1710~61)によって発見された。与えられた区間[a,b]での f(x)の定積分
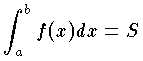 の値が正確に求められないときには,積分が容易に求められる関数,たとえば多項式 p(x)で f(x)を近似して,p(x)の定積分をもって f(x)の定積分の近似値とする方法が用いられる。この方法の一般公式は,ニュートン=コーツの公式で与えられる。シンプソンの公式は,ニュートン=コーツの公式の,n=2の場合にあたり,シンプソンの 1/3則ともいわれる。n=3のときがシンプソンの 3/8則である。区間[a,b]を 2n 等分し,その分点を順に a=x0,x1,x2,…,x2n=b とし,これらに対応する y=f(x)の値をそれぞれ,y0,y1,y2,…,y2n とすれば,定積分 S の近似値は S≅(h/3){y0+4(y1+y3+…+y2n-1)+2(y2+y4+…+y2n-2)+y2n}で与えられる。ただし h=(b-a)/2n である。
の値が正確に求められないときには,積分が容易に求められる関数,たとえば多項式 p(x)で f(x)を近似して,p(x)の定積分をもって f(x)の定積分の近似値とする方法が用いられる。この方法の一般公式は,ニュートン=コーツの公式で与えられる。シンプソンの公式は,ニュートン=コーツの公式の,n=2の場合にあたり,シンプソンの 1/3則ともいわれる。n=3のときがシンプソンの 3/8則である。区間[a,b]を 2n 等分し,その分点を順に a=x0,x1,x2,…,x2n=b とし,これらに対応する y=f(x)の値をそれぞれ,y0,y1,y2,…,y2n とすれば,定積分 S の近似値は S≅(h/3){y0+4(y1+y3+…+y2n-1)+2(y2+y4+…+y2n-2)+y2n}で与えられる。ただし h=(b-a)/2n である。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
百科事典マイペディア
「シンプソンの公式」の意味・わかりやすい解説
シンプソンの公式【シンプソンのこうしき】
関数f(x)のx=aからbまでの定積分(式1)の近似値を求める一方法。区間[a,b]を2n等分(1区分の長さh=(b−a)/2n)し,各分点をx(/0)(=a),x1,x2,…,x2(/n)(=b),それらを代入したy=f(x)の値をy(/0),y1,y2,…,y2(/n)とするとき,上の積分の近似値は {y(/0)+4(y1+y3+…+y2(/n)(/-)1) +2(y2+y4+…+y2(/n)(/-)2)+y2(/n)}h/3で与えられる。その誤差の絶対値は(b−a)5G/2880n4より小さい(Gはf(x)の第4次微分係数の[a,b]内での最大値)。英国のシンプソンThomas Simpson〔1710-1761〕が発見。
→関連項目数値積分
出典 株式会社平凡社百科事典マイペディアについて 情報
Sponserd by 
法則の辞典
「シンプソンの公式」の解説
シンプソンの公式【Simpson's formula】
定積分を求めるための近似公式.シンプソンの法則*,シンプソンの放物線公式*とも呼ばれる.積分対象となる関数(f(x))の曲線をいくつもの区間に区切って放物線で近似する.積分区間[a,b]を2n 等分し,(b-a)/2n=h として,a,a+h,a+2h,…に相当する f(x) の値をy0,y1,y2,…としたとき,積分の近似値 A は次の式で求められる.
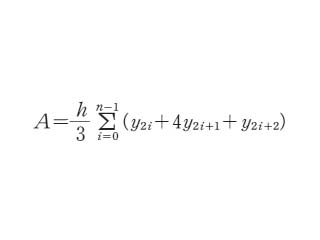
出典 朝倉書店法則の辞典について 情報
Sponserd by 
世界大百科事典(旧版)内のシンプソンの公式の言及
※「シンプソンの公式」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by 
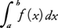 の近似計算のために次のようにして作られた公式である。区間[a,b]を2n等分した分点をa=x0,x1,x2,……,x2n=bとし,それらに対応するf(x)の値をy0,y1,y2,……,y2nとする。n個の小区間[x0,x2],[x2,x4],……,[x2n-2,x2n]において,関数y=f(x)を,それぞれ図におけるf(x)のグラフ上の3点{P0,P1,P2},{P2,P3,P4},……,{P2n-2,P2n-1,P2n}を通る放物線をグラフとする二次関数で置き換え,
の近似計算のために次のようにして作られた公式である。区間[a,b]を2n等分した分点をa=x0,x1,x2,……,x2n=bとし,それらに対応するf(x)の値をy0,y1,y2,……,y2nとする。n個の小区間[x0,x2],[x2,x4],……,[x2n-2,x2n]において,関数y=f(x)を,それぞれ図におけるf(x)のグラフ上の3点{P0,P1,P2},{P2,P3,P4},……,{P2n-2,P2n-1,P2n}を通る放物線をグラフとする二次関数で置き換え,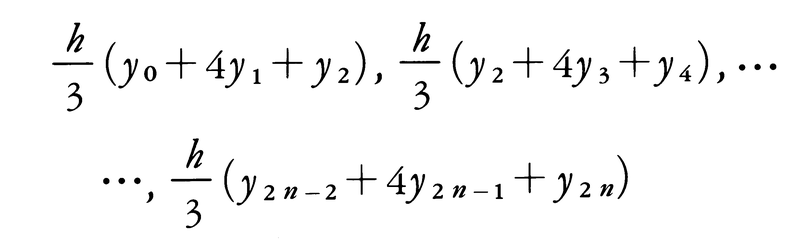
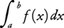
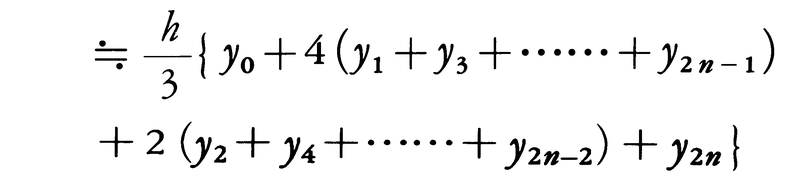
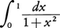 を計算するために,区間[0,1]を10等分すると,n=5,h=0.1,x0=0,x1=0.1,x2=0.2,……,x9=0.9,x10=1であり,対応するyの値から,
を計算するために,区間[0,1]を10等分すると,n=5,h=0.1,x0=0,x1=0.1,x2=0.2,……,x9=0.9,x10=1であり,対応するyの値から,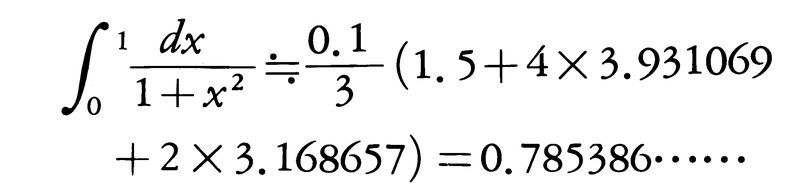


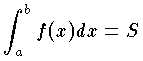 の値が正確に求められないときには,積分が容易に求められる関数,たとえば多項式 p(x)で f(x)を近似して,p(x)の定積分をもって f(x)の定積分の
の値が正確に求められないときには,積分が容易に求められる関数,たとえば多項式 p(x)で f(x)を近似して,p(x)の定積分をもって f(x)の定積分の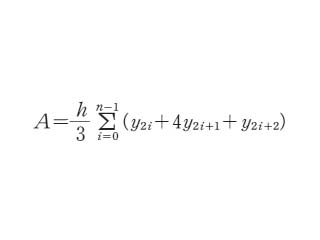
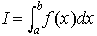 は,f(x)の不定積分F(x)がわかれば,ただちにF(b)-F(a)として求まるが,F(x)がうまく求まらないとき多項式のように定積分が容易にわかる関数p(x)でf(x)を近似して,p(x)の積分をIの近似値とする。その近似値を数値的に求めるのが数値積分である。Iをより一般に,正の値をとる重み関数w(x)をつけて,
は,f(x)の不定積分F(x)がわかれば,ただちにF(b)-F(a)として求まるが,F(x)がうまく求まらないとき多項式のように定積分が容易にわかる関数p(x)でf(x)を近似して,p(x)の積分をIの近似値とする。その近似値を数値的に求めるのが数値積分である。Iをより一般に,正の値をとる重み関数w(x)をつけて,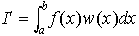 の形で扱われることが多い。I′の近似値が,
の形で扱われることが多い。I′の近似値が,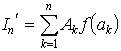 と表されるとき,akは標本点,Akは重みと呼ばれる。…
と表されるとき,akは標本点,Akは重みと呼ばれる。…