改訂新版 世界大百科事典 「数値積分」の意味・わかりやすい解説
数値積分 (すうちせきぶん)
numerical integration
関数f(x)の定積分,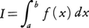 は,f(x)の不定積分F(x)がわかれば,ただちにF(b)-F(a)として求まるが,F(x)がうまく求まらないとき多項式のように定積分が容易にわかる関数p(x)でf(x)を近似して,p(x)の積分をIの近似値とする。その近似値を数値的に求めるのが数値積分である。Iをより一般に,正の値をとる重み関数w(x)をつけて,
は,f(x)の不定積分F(x)がわかれば,ただちにF(b)-F(a)として求まるが,F(x)がうまく求まらないとき多項式のように定積分が容易にわかる関数p(x)でf(x)を近似して,p(x)の積分をIの近似値とする。その近似値を数値的に求めるのが数値積分である。Iをより一般に,正の値をとる重み関数w(x)をつけて,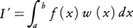 の形で扱われることが多い。I′の近似値が,
の形で扱われることが多い。I′の近似値が,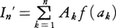 と表されるとき,akは標本点,Akは重みと呼ばれる。標本点a0,a1,……,anが与えられたときf(x)の近似関数fn(x)として,ラグランジュの補間多項式が用いられることが多い。それは各kについて,
と表されるとき,akは標本点,Akは重みと呼ばれる。標本点a0,a1,……,anが与えられたときf(x)の近似関数fn(x)として,ラグランジュの補間多項式が用いられることが多い。それは各kについて,
fn(ak)=f(ak)
となるn次多項式で,次に示す式で与えられる。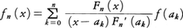 ただしFn(x)=(x-a0)(x-a1)……(x-an)。そのとき,
ただしFn(x)=(x-a0)(x-a1)……(x-an)。そのとき,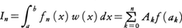 で,
で,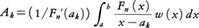 である。これを補間型積分公式という。具体的な応用にあたっては標本点の選び方が問題になる。よく知られている場合として,ニュートン=コーツの公式を用いる方法と,ガウスの公式を利用するものなどがある。
である。これを補間型積分公式という。具体的な応用にあたっては標本点の選び方が問題になる。よく知られている場合として,ニュートン=コーツの公式を用いる方法と,ガウスの公式を利用するものなどがある。
ニュートン=コーツの公式
w(x)≡1の場合で区間[a,b]のn等分点a=a0<a1<……<an=bを標本点とする。ラグランジュの補間多項式fn(x)は,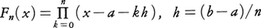 から求められる。このときIの近似,
から求められる。このときIの近似,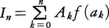 における重みは,
における重みは,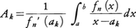 である。とくにn=1のときが台形公式,
である。とくにn=1のときが台形公式,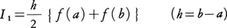 n=2のときがシンプソンの1/3公式,
n=2のときがシンプソンの1/3公式,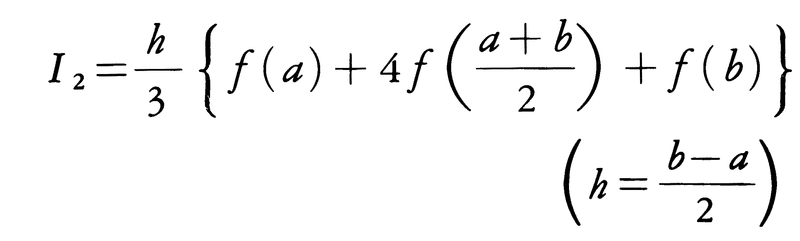
n=3のときがシンプソンの3/8公式,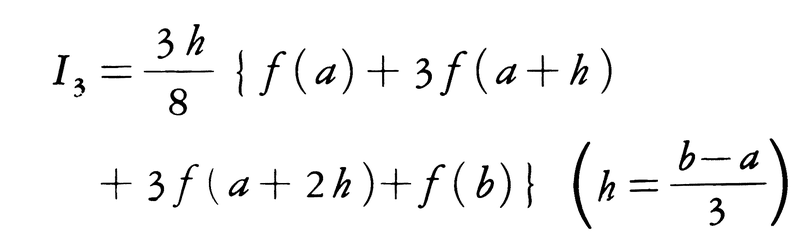
である。よりよい近似を得るため,実際は[a,b]を多くの小区間に等分し,各小区間でn次多項式fn(x)を用いる複合則を適用する。上記ニュートン=コーツの公式に対し,分割した小区間の中点での値を用いたマクローリンの公式もよく知られている。
ガウスの公式
重み関数w(x)をつけた,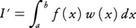 を扱う。w(x)に関して定義される直交多項式をpn(x)(n≧0)とし,pn(x)の零点をa1,a2,……,anとする。これらについては正定数wjとλkが定まって,
を扱う。w(x)に関して定義される直交多項式をpn(x)(n≧0)とし,pn(x)の零点をa1,a2,……,anとする。これらについては正定数wjとλkが定まって,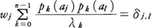 をみたす。これからラグランジュの補間多項式,
をみたす。これからラグランジュの補間多項式,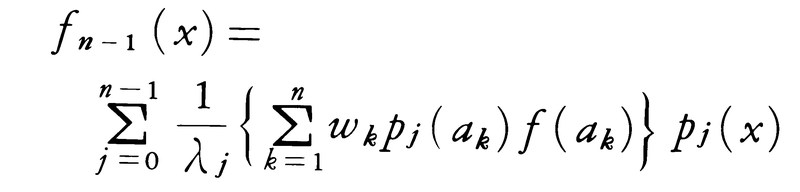
が得られ,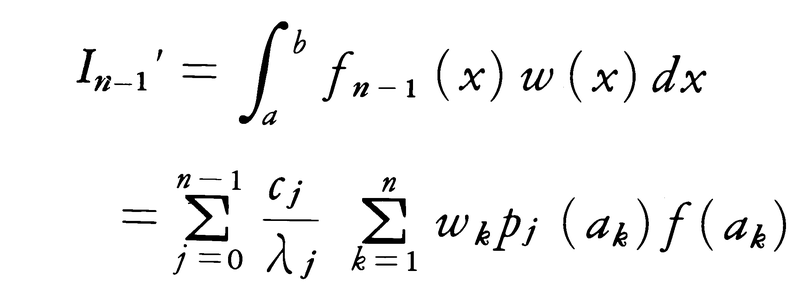
が求められる。ここで,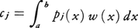 である。
である。
執筆者:飛田 武幸
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報

