翻訳|error
精選版 日本国語大辞典 「誤差」の意味・読み・例文・類語
ご‐さ【誤差】
- 〘 名詞 〙
- ① 真の値(厳密値)とその近似値または測定値との差。
- [初出の実例]「紙幣の国内に通布する内に、断残し、或は交換し、或は誤差にて不用となりたるを、点検の後に切断し」(出典:米欧回覧実記(1877)〈久米邦武〉一)
- ② 食い違い。狂い。
- [初出の実例]「わづかの誤差が全姿を破壊してしまふ」(出典:私の美術遍歴(1956)〈亀井勝一郎〉観音菩薩像)
改訂新版 世界大百科事典 「誤差」の意味・わかりやすい解説
誤差 (ごさ)
error
測定,理論的推定,近似計算などの結果として得られた値と真実の値との差。諸量の測定値の誤差を数学的に取り扱う誤差論は,1800年代の初めにC.F.ガウスによって始められた。その主要な内容は彼自身によって完成されたといってよいほどで,同じガウスにより創始された最小二乗法と表裏をなすものである。この両理論は幅広いガウスの研究の基本的な道具となった。彼は太陽のまわりを回る天体の運動を論ずるにあたり,きわめて多数の観測を行ったが,その観測値の誤差の処理の重要さを知って,天体運動論と同時に誤差論をも確立した。
測定値の誤差は規則的なものと偶発性のものとに分けられる。前者は人為的に容易に処理されるが,むずかしいのは後者で,その取扱いには確率論が必要となる。それは偶然誤差と呼ばれ連続的な値をとる確率変数と考えられる。その分布の密度関数をφ(x)とかく。平均値は規則的な誤差の中にくり込んでよいので,偶然誤差の平均値はいつも0としてよい。すなわち,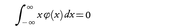 である。また多くの場合,平均値を中心にして過不足は同程度の割合で起こるとしてよいのでφ(-x)=φ(x)と仮定する。この分布の二次のモーメント,
である。また多くの場合,平均値を中心にして過不足は同程度の割合で起こるとしてよいのでφ(-x)=φ(x)と仮定する。この分布の二次のモーメント,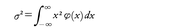 の平方根,すなわち標準偏差σは誤差論では平均誤差と呼ばれる。そしてその逆数1/σは精密さを表す。平均誤差はP.S.ラプラスのように誤差の絶対値の平均,
の平方根,すなわち標準偏差σは誤差論では平均誤差と呼ばれる。そしてその逆数1/σは精密さを表す。平均誤差はP.S.ラプラスのように誤差の絶対値の平均, を用いてもよいが,ガウスのようにσを用いるほうが以後の解析を進めるうえで好つごうである。さて,誤差の分布,すなわちφ(x)の関数形であるが,ガウスは誤差のもつ性質から演繹して,正規分布(ガウス分布)がもっとも自然であることを理論的に示した。それは,
を用いてもよいが,ガウスのようにσを用いるほうが以後の解析を進めるうえで好つごうである。さて,誤差の分布,すなわちφ(x)の関数形であるが,ガウスは誤差のもつ性質から演繹して,正規分布(ガウス分布)がもっとも自然であることを理論的に示した。それは,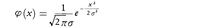 で,σが平均誤差である。この他に区間[-a,a]上の一様分布,
で,σが平均誤差である。この他に区間[-a,a]上の一様分布, も登場することがある。例えば連続量を四捨五入して整数値に丸める場合で,端数は-0.5から+0.5まで一様に分布していると考えられる。このとき平均誤差σは1/(2\(\sqrt{3}\))となる。一般に[-a,a]上の一様分布ならσ=a/\(\sqrt{3}\)である。正規分布や一様分布では,平均誤差σを知れば,その分布が完全に決定されるので,誤差がある範囲にとどまる確率はすぐに知られる。正規分布のときなら区間[aσ,bσ]に入る確率は標準正規分布の表から区間[a,b]内にある確率を見ればすぐにわかる。一般のφ(x)の場合でも,関数φ(x)が|x|が増加するにつれて減少する性質をもつ場合には,λを正数として,誤差が区間[-λσ,λσ]にとどまる確率μとλとの間には,
も登場することがある。例えば連続量を四捨五入して整数値に丸める場合で,端数は-0.5から+0.5まで一様に分布していると考えられる。このとき平均誤差σは1/(2\(\sqrt{3}\))となる。一般に[-a,a]上の一様分布ならσ=a/\(\sqrt{3}\)である。正規分布や一様分布では,平均誤差σを知れば,その分布が完全に決定されるので,誤差がある範囲にとどまる確率はすぐに知られる。正規分布のときなら区間[aσ,bσ]に入る確率は標準正規分布の表から区間[a,b]内にある確率を見ればすぐにわかる。一般のφ(x)の場合でも,関数φ(x)が|x|が増加するにつれて減少する性質をもつ場合には,λを正数として,誤差が区間[-λσ,λσ]にとどまる確率μとλとの間には,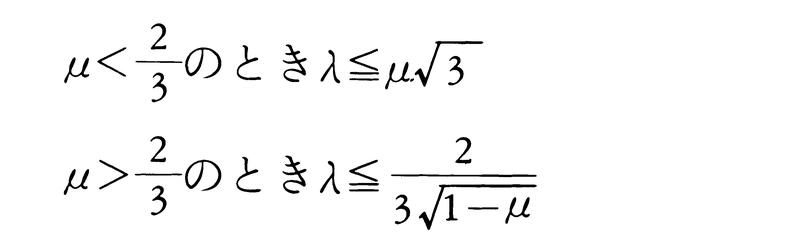
なる関係がある。これはチェビシェフの不等式を用いるよりもよい評価を与えている。また誤差の評価には四次のモーメントm4=∫x4φ(x)dxもよく用いられる。平均誤差σの正規分布のときはm4=3σ2で,[-a,a]上の一様分布ならm4=a4/5である。
いまx1,x2,……,xnを互いに独立な同一種類の観測値の誤差を表すとしよう。これらは同じ分布の密度関数φ(x)をもつ独立な確率変数の実現値とみなされる。それらの誤差がそれぞれ区間[a1,b1],[a2,b2],……,[an,bn]の中にある確率は積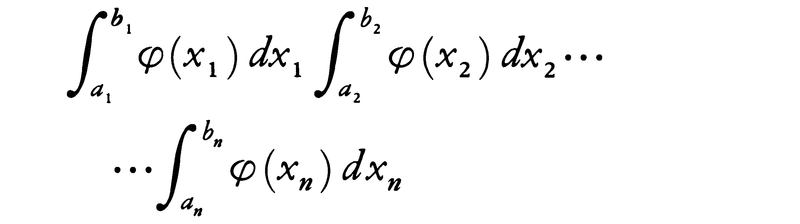
で表され,したがって,これらの誤差の関数y=f(x1,x2,……,xn)の平均値は,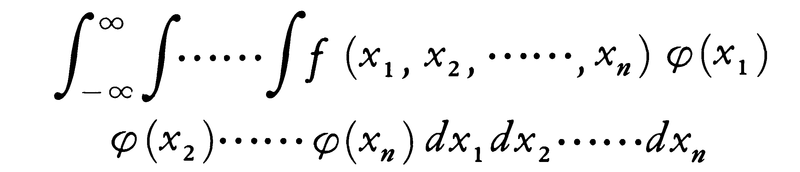
となる。とくに各xiの平均誤差がσであるとき,yが各誤差の平方の算術平均(x12+x22+……+xn2)/nなら,yの平均値はやはりσ2である。しかしyの偶然の値が平均値σ2からどの程度近いかという確からしさは,数nが増せば増すほど大きくなる。それはy=σ2と想定するときの平均誤差を計算することによって実証できる。実際,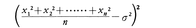 の平均値を求めると(m4-σ4)/nとなり,nが大きければこれは無視できるほどの小さな量である。すなわち十分多くの独立で同種の偶然誤差x1,x2,……,xnがあれば,σ2の近似値がそれらの平方の算術平均でもって,十分な確かさで求まることがわかる。こうしてσ2を決めるとき,それに対する平均誤差は
の平均値を求めると(m4-σ4)/nとなり,nが大きければこれは無視できるほどの小さな量である。すなわち十分多くの独立で同種の偶然誤差x1,x2,……,xnがあれば,σ2の近似値がそれらの平方の算術平均でもって,十分な確かさで求まることがわかる。こうしてσ2を決めるとき,それに対する平均誤差は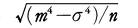 にしかすぎない。
にしかすぎない。
これまで,いくつかの観測値は同種のものとして扱ってきたが,今度は誤差x1,x2,……,xnは異種のもので異なった精密さをもっているとする。それらの分布は異なった関数φ1(x1),φ2(x2),……,φn(xn)によって表され,平均誤差がそれぞれσ1,σ2,……,σnだとする。このとき和x12+x22+……+xn2の平均値はσ12+σ22+……+σn2である。いま各誤差の平均誤差がそれぞれ1,k2,k3,……,knに比例しているとすれば,
(x12+x22+……+xn2)/(1+k22+k32+……+kn2)
の平均値はσ12である。あるいは,このとき上式からnを大きくしてσ12が,したがってσ22=k22σ12,……,σn2=kn2σ12が求まることがわかる。このσ12の確定値に対する平均誤差は前と同様,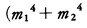
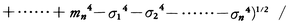
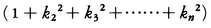 に等しいことが示される。さらにm1,m2,……,mnがσ1,σ2,……,σnに比例すると仮定すれば(正規分布のときはこの仮定が成り立つ),上の平均誤差は,
に等しいことが示される。さらにm1,m2,……,mnがσ1,σ2,……,σnに比例すると仮定すれば(正規分布のときはこの仮定が成り立つ),上の平均誤差は,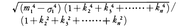 となる。
となる。
これまでのことを基礎にして,Uが未知量V1,V2,……,Vnの関数で,各Viが誤差eiを伴った観測値とするとき,Uの誤差について調べよう。各Viの小さな変化δViに応ずるUの変化δUは,近似的に和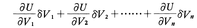 で表される。ゆえにUの値の誤差EはViの誤差eiを用いて近似的に,
で表される。ゆえにUの値の誤差EはViの誤差eiを用いて近似的に,
E=λ1e1+λ2e2+……+λnen
で表される。ここでλiはViの真の値における偏微分係数∂U/∂Viである。そして観測は各誤差の平方や積が無視される程度に小さいものとする。観測誤差の平均値は0にしてあるので,Eの平均値は当然0で,E2の平均値M2はUの誤差の平均誤差の平方に等しい。具体的な値はeiの平均誤差をσiとすれば,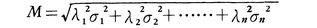 となる。ところでλiの真の値は一般に知られないことが多いので,誤差は小さいと考えてλiの代りに∂U/∂Viの観測値Viにおける値を用いてよい。またこの場合,観測値の平均誤差の代りに観測の重みを用いることがある。適当な単位を選んで,V1,V2,……,Vnの観測値の重みをp1,p2,……,pnとするとき,Uの値の重みをPとかけば,
となる。ところでλiの真の値は一般に知られないことが多いので,誤差は小さいと考えてλiの代りに∂U/∂Viの観測値Viにおける値を用いてよい。またこの場合,観測値の平均誤差の代りに観測の重みを用いることがある。適当な単位を選んで,V1,V2,……,Vnの観測値の重みをp1,p2,……,pnとするとき,Uの値の重みをPとかけば,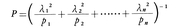 である。同じ未知量V1,V2,……,Vnの他の関数Tが与えられたとして,α1,α2,……,αnをそれぞれ,
である。同じ未知量V1,V2,……,Vnの他の関数Tが与えられたとして,α1,α2,……,αnをそれぞれ,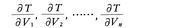 の真の値V1,V2,……,Vnにおける値とする。V1,V2,……,Vnの観測値からTの値を推定するときの誤差E′は和α1e1+α2e2+……+αnenで表され,その平均誤差は,
の真の値V1,V2,……,Vnにおける値とする。V1,V2,……,Vnの観測値からTの値を推定するときの誤差E′は和α1e1+α2e2+……+αnenで表され,その平均誤差は, である。注意すべきことは,上のEとこのE′とは独立ではなく,積EE′の平均値は個々のeiなどの場合と違って0にはならない。実は,EE′の平均値はλ1α1σ12+λ2α2σ22+……+λnαnσn2である。
である。注意すべきことは,上のEとこのE′とは独立ではなく,積EE′の平均値は個々のeiなどの場合と違って0にはならない。実は,EE′の平均値はλ1α1σ12+λ2α2σ22+……+λnαnσn2である。
今度は,上に出てきた量V1,V2,……,Vnが未知量x1,x2,……,xlの関数であるとしよう。独立になされた観測によって,V1,V2,……,Vnの値がそれぞれL1,L2,……,Lnとして求められたとき,未知量を決定する方法を考える。lがnより大きいときは明らかに不定の問題となる。もしl=nなら個々のxiは一般にV1,V2,……,Vnの関数として表される。そこでxi=Uとみて前の結果を使うことができる。とくに各Viがx1,x2,……,xnの一次関数である場合には詳しい議論ができる。まず話を簡単にするための変形をしよう。V1=L1,V2=L2,……,Vn=Lnを確定するときの平均誤差をそれぞれσ1,σ2,……,σn,この確定の重みをp1,p2,……,pn(したがってp1σ12=p2σ22=……=pnσn2である)として,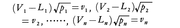 とおく。このとき,初めの問題は,平均誤差が
とおく。このとき,初めの問題は,平均誤差が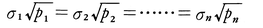 あるいは重みが1である同じ精密さの観測値から,
あるいは重みが1である同じ精密さの観測値から,
v1=0,v2=0,……,vn=0
という結果が得られたとするのと同じ設定になる。そこで一般に,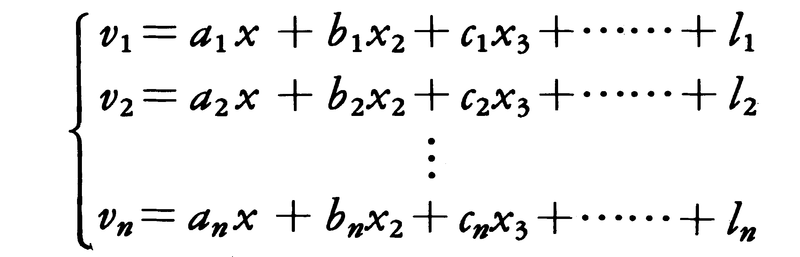
であったとして,
κ1v1+κ2v2+……+κnvn=x-k
で与えられる係数の組κ1,κ2,……,κnのうちで和κ12+κ22+……+κn2を最小にするものを見つけたい。そのため次のような変形をする。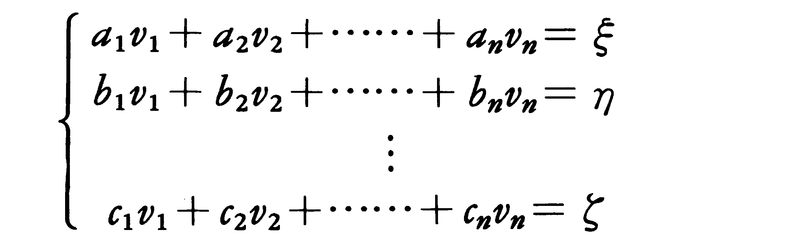
とおけば,ξ,η,……,ζはすべてx1,x2,……,xnの一次関数で表される。それを解いて,
x1=A+[α1α1]ξ+[α1α2]η+……+[α1αn]ζ
のように記すのが好つごうである。ただし係数[α1αi]は,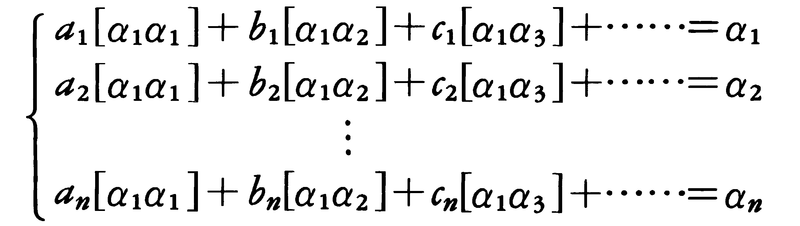
で決まる。そして,
α1v1+α2v2+……+αnvn=x1-A
が成り立つ。κ1,κ2,……,κnについての等式を用いて,
(κ1-α1)v1+(κ2-α2)v2+……+(κn-αn)vn=A-k
が得られ,これから,
(κ1-α1)α1+(κ2-α2)α2+……+(κn-αn)αn=0
が知られる。これを書き直せば,
κ12+κ22+……+κn2=α12+α22+……+αn2+(κ1-α1)2+(κ2-α2)2+……+(κn-αn)2
となる。これから左辺の最小値がκ1=α1,κ2=α2,……,κn=αnのときに実現されることがわかる。さて,元の特殊な場合にかえり,等式v1=0,v2=0,……,vn=0が得られたとする。未知の量x1を求めるために,x1の係数は1で他のx2,x3,……,xnが消去されるように組み合わせた式,
κ1v1+κ2v2+……+κnvn=0
が求められる。この確定の重みは(κ12+κ22+……+κn2)⁻1で,κ1=α1,κ2=α2,……,κn=αnとおいて目的の確定値x1=Aを得る。残りの変数についても同様である。いまΩ=p1(V1-L1)2+p2(V2-L2)2+……+pn(Vn-Ln)2とおけば,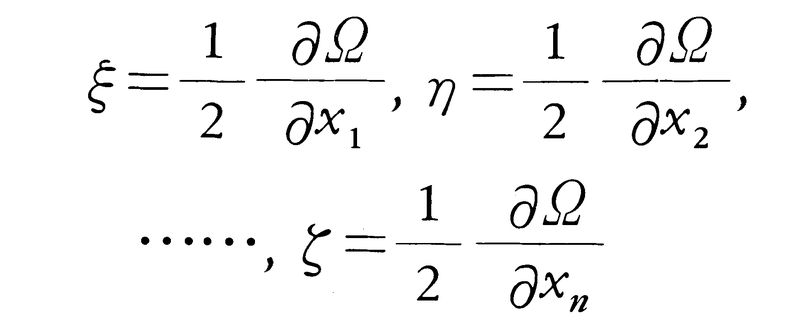
であり,われわれはそれらを0にすることによって,x1,x2,……,xnの確定値を得たことになる。
→測定誤差
執筆者:飛田 武幸
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「誤差」の意味・わかりやすい解説
誤差
ごさ
error
測定をしたり計算をしたりするとき、本当に知りたいのは真値(厳密値)であるが、実際にはそれに近い値(近似値)しか得られないことが多い。両者の差を誤差という。符号をつけて表すときは、近似値のほうが大きい場合(過大近似値の場合)をプラスにとるのが普通である。式で表せば次のようになる。
(近似値)-(真値)=(誤差)
[戸川隼人]
誤差の尺度
誤差の大きさを表すには、前記の値の絶対値(これを絶対誤差という)をそのまま用いてもよいが、真値に対する割合で表すほうが適当なこともある。これを相対誤差という。
|(近似値)-(真値)|=(絶対誤差)
また、一つの値だけを問題にするのではなく、いくつかの値の組を問題にする場合には、個々の値の誤差のほかに、総合的な誤差の尺度として、誤差の総和、誤差の二乗和、誤差の平均値、誤差の最大値などが用いられる。
[戸川隼人]
誤差の性質
誤差には、規則性のあるものと、まったく不規則(ランダム)なものとがある。このうち、規則性のあるものに関しては、十分に調べれば補正できることが多い。ただし、原因は多種多様なので、対策はケース・バイ・ケースである。不規則な誤差に関しては、一見どうしようもないように思えるが、多くの場合、誤差がある種の確率分布に従う。この分布は正規分布またはガウス分布とよばれている。この種の誤差については確率論を用いて性質を研究することができ、たとえば「同じものをN回測定して平均すれば、平均値の誤差の期待値は元の誤差の1/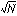 になる」ということなどが知られている。
になる」ということなどが知られている。
[戸川隼人]
誤差の伝播
誤差を含むデータに計算処理を行うと、計算結果にも誤差が入る。その影響に関しては次のようなことがいえる。加減算すると絶対誤差は元の誤差の和になる。相対誤差は、普通はあまり変わらないが、符号が反対で絶対値がほぼ等しい二つの数を加えるような場合には相対誤差が急増する。これを桁(けた)落ちという。乗除算結果の相対誤差は、元の値の相対誤差の和にほぼ等しい。ただし除数の相対誤差が大きい場合には、誤差が著しく拡大されることがある。方程式の係数や定数項に誤差が含まれていると、方程式の解に誤差が入る。その影響の大小は方程式の性質によって決まる。わずかの誤差が結果に大きな影響を与えるならば、悪条件ill-conditionであるという。
[戸川隼人]
数値計算の誤差
数値計算における誤差には大別して丸めの誤差と打ち切り誤差がある。丸めの誤差は数値を有限桁数で扱うために生ずる。打ち切り誤差は、無限級数の和を有限項の和で近似したり、逐次近似法の反復を途中で打ち切ったり、微積分を離散的に近似したりする際に生ずる。
[戸川隼人]
『戸川隼人著『誤差解析の基礎』(1974・サイエンス社)』▽『ウィルキンソン著、一松信・四条忠雄訳『基本的演算における丸め誤差解析』(1974・培風館)』▽『永坂秀子著『計算機と数値解析』(1980・朝倉書店)』▽『吉沢康和著『新しい誤差論――実験データ解析法』(1989・共立出版)』▽『大石進一著『精度保証付き数値計算』(2000・コロナ社)』
百科事典マイペディア 「誤差」の意味・わかりやすい解説
誤差【ごさ】
→関連項目近似値
出典 株式会社平凡社百科事典マイペディアについて 情報
岩石学辞典 「誤差」の解説
誤差
化学辞典 第2版 「誤差」の解説
誤差
ゴサ
error
真の値からの測定値のずれを誤差という.真の値が不明なときは,測定値から真の値を推定しなくてはならないので,数学的取り扱いが必要になる.これを誤差解析という.最小二乗法はその一例である.このような数学の対象となる誤差は偶然誤差であって,環境や測定装置による偏りから生じる系統誤差は,誤差解析の対象にはなりにくい.
出典 森北出版「化学辞典(第2版)」化学辞典 第2版について 情報
ブリタニカ国際大百科事典 小項目事典 「誤差」の意味・わかりやすい解説
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
栄養・生化学辞典 「誤差」の解説
誤差
世界大百科事典(旧版)内の誤差の言及
【郵便切手】より
…この穴のないものを無目打imperf,角の目打のとれたものを目打欠,目打が正しい位置からずれているものを目打ずれという。 エラーerrorまちがって作られた切手をいい,図案の誤り,文字の誤り,刷色の誤りなどがある。 すかしwatermark偽造を防ぐために切手の紙に文字や模様のすかしを入れたもので,日本では以前にはすかしを入れたこともあるが現在の切手にはない。…
【近似値】より
…また1mm単位の目盛のものさしで長さを測ったときの測定値,コンピューターで用いるデータの離散化なども近似値の取扱いになる。真の値と近似値との差を誤差と呼ぶ。いろいろな量を測定する場合に,真の値が正確にはわからないときは誤差もわからないが,そのような場合でも誤差の限界はわかる場合が多い。…
【測定】より
…測定のために援用した法則自身の,あるいはそれを測定系によって実現する際の不完全さや,測定時における環境変動など外部からのじょう乱などのために,信号の質が低下したりゆがめられたりして測定値として“真の値”と異なる値が得られることが多い。測定値から真の値を差し引いた値を誤差というが,これは概念規定である。真の値がわかっていれば測定の必要はなく,わからなければ誤差が求まらない。…
【測定誤差】より
…測定の目的は測定量の真の値を求めることであるが,得られる測定値にはいくらかの誤差が含まれることは避けられない。このように測定に際して測定値に入りこむ誤差を測定誤差と呼び,測定値から真の値を引いた値と定義する。…
※「誤差」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...

