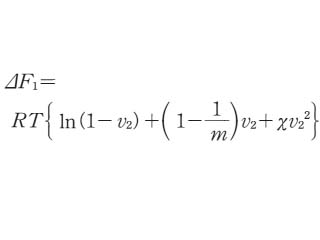化学辞典 第2版 の解説
フローリー-ハギンスの理論
フローリーハギンスノリロン
Flory-Huggins' theory
高分子溶液の混合エントロピーが異常に大きいのは,溶質の分子量が大きいためである.そこで,N0 個の溶媒分子と N1 個の溶質分子からなり,各溶質分子はそれぞれn個のセグメントからなる系について,ブラッグ-ウィリアムズ近似を用いて,P.J. Flory(フローリー)は混合エントロピーとして,
k(N0 ln φ0 + N1 ln φ1)
を導いた.ただし,kはボルツマン定数,φ0,φ1 は溶媒,高分子の容積分率で,
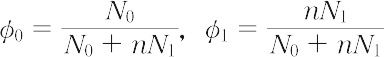
で与えられる.この混合エントロピーの式は,φ0,φ1 をモル分率とみなせば,形式的には理想溶液に対するものと同じで,簡単な形をしている.M.L. Hugginsは高分子がつながっている効果をさらに精密に取り入れて,少し違った形の式を得た.しかし,混合自由エネルギーの形で表すと,二つの理論は同一の形になるので,両者を合わせてフローリー-ハギンスの理論という.
出典 森北出版「化学辞典(第2版)」化学辞典 第2版について 情報