精選版 日本国語大辞典 「自由エネルギー」の意味・読み・例文・類語
じゆう‐エネルギージイウ‥【自由エネルギー】
- 〘 名詞 〙 ( エネルギーは[ドイツ語] Energie ) 仕事に転換することのできるエネルギー。系の内部エネルギーから、その絶対温度とエントロピーの積を引いたもの。
日本大百科全書(ニッポニカ) 「自由エネルギー」の意味・わかりやすい解説
自由エネルギー
じゆうえねるぎー
物体(熱力学的な体系、以下単に「体系」とよぶ)のもつ内部的なエネルギーの一種で、物体が一定の温度に保たれたまま(等温過程)で、外部に仕事として取り出し可能なエネルギーを自由エネルギーとよんでいる。もちろん物体全体の並進や回転運動のエネルギーは除かれている。正確にはヘルムホルツの自由エネルギーというが、以下しばらくは単に自由エネルギーと称する。
[小野昱郎]
断熱過程と等温過程
気体は膨張するときに、外部に仕事をすることができる。この過程が熱の出し入れなしに行われたときは(断熱過程)、気体のもつ内部エネルギーは、外部に仕事をした分だけ失われる。このとき、気体の温度も一般に低下する。一方、熱の出入りが許されたとき(非断熱的)、外部から自然に熱が流れ込み、失った内部エネルギーが補われる。とくに、希薄気体(理想気体)を一定の温度に保ったときは(等温過程)、外部に仕事した分、減少した内部エネルギーは、流れ込んだ熱量で完全に補われ、結局内部エネルギーは一定に保たれる。この点、ばねの伸縮による弾性エネルギーとは異なっている。一方、自由エネルギーは等温過程で膨張したとき、外部に仕事をした分だけ失われ、逆に圧縮されるとき、外部からもらった仕事の分だけ増加する。
[小野昱郎]
内部エネルギー
熱力学第一法則に従うと、物体の内部エネルギーUの増加ΔUは一般に外部からもらった熱ΔQと外部からもらった仕事ΔWの和であり、
ΔU=ΔQ+ΔW (1)
と表される。これらの量は正負の符号をもつ。ΔUが正なら内部エネルギーの増加、負ならば減少を表す。ΔQは正ならもらった熱、負ならば出した熱である。同様に、ΔWが正ならば外部からもらった仕事、負ならば外部へした仕事になる。気体の場合、ゆっくりと(可逆的に)ΔVだけ膨張したときは(ΔV>0)、気体の圧力をpとすれば、外部へpΔVの仕事をする。外部へした仕事は負の量だから、ΔW=-pΔVと表され、(1)式は
ΔU=ΔQ-pΔV (2)
となる。断熱過程では、熱の出入りはなくΔQ=0であるから、内部エネルギーはpΔVだけ減少することがわかる。
一方、希薄な気体(理想気体)の内部エネルギーはその温度Tのみに依存して、体積Vにはよらないことが、実験的に示されている。したがって、気体の等温過程では、つねにΔU=0となるから、外部からもらった熱ΔQは外部へした仕事pΔVと等しいことが(2)式を用いて示される。気体が等温的に膨張し、外部に仕事をしても、内部エネルギーは減少しないことがわかった。
[小野昱郎]
ヘルムホルツの自由エネルギー
自由エネルギーFは
F=U-TS (3)
のように定義される。ここで、Tは物体の絶対温度、Sはそのエントロピーである。等温過程では温度Tが一定であるので、自由エネルギーの変化ΔFは(3)式より
ΔF=ΔU-TΔS (4)
(2)式を用いて、さらに、熱の出入りがゆっくりと可逆的に行われたとき、エントロピーの増加はΔS=ΔQ/Tで与えられるので、
ΔF=ΔQ-pΔV-TΔS
=-pΔV (5)
となる。したがって、等温可逆過程では、自由エネルギーの変化ΔFは-pΔV、つまり外部から圧縮(ΔV<0)によってもらった仕事量だけ増加し、膨張(ΔV>0)によって外部にした仕事量だけ減少することが証明される。
一般に物体を等温に保ちながら、熱力学的変化をおこさせ、外部と可逆的に仕事のやりとりがあったとき、それに見合った物体のエネルギーの変化は自由エネルギーの変化であり、内部エネルギーの変化ではない。一方、物体と外部が断熱されているときは、内部エネルギーの変化になる。
[小野昱郎]
熱力学関係式
一般に物体の温度も体積も微小変化をしたときの自由エネルギーの微小変化を考えよう。以下では、微小変化をdと表す。(3)式とdQ=TdSを用いて
dF=dU-d(TS)
=dQ-pdV-TdS-SdT
=-pdV-SdT (6)
となる。Sは正であるから、温度が上昇すると、自由エネルギーは減少することがわかる。dT=0とすると、(6)式より物体の圧力pは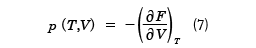
と計算することができる。FがT,Vの関数として与えられているとき、(7)式はp、T、Vの間の関係式で、物体の状態方程式を与える。ここで、( )Tは温度Tが一定で、もう一つの変数で偏微分することを表している。また、エントロピーSはdV=0と置いて、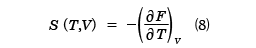
と求めることができる。さらに、定積熱容量CVはSを用いて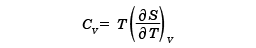
で与えられる。ほかに、定圧熱容量、膨張率、圧縮率など、必要な熱力学的な量はすべて計算することができる。
熱統計力学で定義されている絶対温度Tの体系の状態和または分配関数をZと書けば、自由エネルギーはF=-kTlogZと表すことができる。ここで、kはボルツマン定数である。したがって、分配関数をTとVの関数として得られれば、自由エネルギーも求めることができることになる。
[小野昱郎]
熱体系の変化の方向
エントロピーの意義の一つは熱体系全体の変化の進む方向を決めることである。たとえば、高温と低温の物体を接触させたとき、高温の物体から低温の物体に熱が流れ、やがて両物体が同じ温度の熱平衡になってしまう。このとき全体系のエントロピーは増大する。これは孤立系で一般に成り立つ「エントロピー増大則」の一例である。この逆の過程は自然にはおこることはないので、系の変化の方向が決まる。
温度が一定に保たれていても、系は変化することがある。このとき自由エネルギーは減少する。一例をあげる。一定の温度に保たれ、間仕切り壁のある容器の左と右側に入れられた二つの気体がある。その気体の圧力が異なるとき、間の壁が可動なら、圧力の高い気体の体積が膨張し、圧力の低い気体の体積が減少するように壁が動き、やがて両気体の圧力が同じになるように自然に変化する。このような等温非可逆過程で、変化後の熱平衡になったときの全自由エネルギーは変化前に比べて低くなることが示される。温度が一定に保たれているとき、自由エネルギーが最小となる状態が、一般に熱平衡状態であるということができる。
[小野昱郎]
ギブスの自由エネルギー
もう一つの自由エネルギーはギブスの自由エネルギーGである。Gは熱力学ポテンシャルとよばれることもある。その定義は、ヘルムホルツの自由エネルギーにpVを加えた
G=F+pV
=U-TS+pV (9)
である。ここで、pは圧力を表している。Gの微小変化dGは(6)式を用いると
dG=dF+d(pV)
=-SdT-pdV+pdV+Vdp
=-SdT+Vdp (10)
GをTとpの関数で表したとき、この式から、等圧変化(dp=0)では、温度の上昇はギブスの自由エネルギーを減少させる。また等温変化(dT=0)で圧力を増加させることは、このエネルギーを増加させることがわかる。しかし、外部への仕事と直接に関係づけられるわけではない。この式から得られる熱力学関係式はdT=0と置くことにより、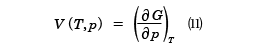
また、(10)式からdp=0と置いて、エントロピー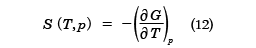
が得られる。(11)式は(7)式と同等な状態方程式であり、(12)式は(8)式と同じSを与える関係式であるが、独立変数がT,VからT,pにかわっている。
[小野昱郎]
化学ポテンシャル
ギブスの自由エネルギーGから直接得られる重要な熱力学量は化学ポテンシャルμ(ミュー)である。均質な体系の場合は、そのモル数をNとして
μ(T,p)=G/N (13)
で定義される。化学ポテンシャルμは1モル当りのギブスの自由エネルギーであり、温度Tと圧力pの関数で表される。μは温度、圧力、密度と同じように物体の量によらない熱力学変数である。これを示強変数とよぶ。一方、物体の量に比例する熱力学変数を示量変数とよぶ。たとえば、体積V、内部エネルギーU、両自由エネルギーF、Gなどがある。
温度と圧力が指定されたとき、ギブスの自由エネルギーは熱平衡状態で最小値をとり、非平衡状態での値と比べるとつねに小さい。つまり、等温かつ等圧では、非平衡状態はGが小さくなる方向へ変化していくことになる。たとえば、相転移で、二つのA、B相(たとえば液相と気相)が接しているとき、各相での化学ポテンシャルをそれぞれμA,μB、各相のモル数をNA,NBとすれば、全体のギブスの自由エネルギーは
G=μANA+μBNB
と表される。各相のモル数の微小変化をそれぞれdNA,dNBとすれば、Gの微小変化dGは
dG=μAdNA+μBdNB
=(μA-μB)dNA (14)
と与えられる。第1式から第2式へは、たとえば、水と水蒸気のように、相が変わっても、化学組成が変わらなければ、全体のモル数は変わらないので、
dNA=-dNB (15)
が成り立つからである。μA>μBのときは、dNA<0(当然dNB>0)でdGは負となり、Gは減少することになる。つまり、A相のモル数は減少しB相は増加する。一般に、一定の温度かつ一定の圧力下で、2相が接しているとき、化学ポテンシャルの高い相から低い相へ物質は移動する。これにより、全体のギブス自由エネルギーは減少する。μA=μBのとき、つまり両相の化学ポテンシャルが等しいときは、両相は共存して、両相の量は任意にとることができる。つまり全体のギブス自由エネルギーは両相の量にはよらず一定である。
[小野昱郎]
なお、化学においてはヘルムホルツの自由エネルギーと、ギブスの自由エネルギーとがある。一定温度、一定圧下での反応系のギブスの自由エネルギーGは、原系から生成系へと自然に反応が進行する場合にはしだいに減少し、反応系が平衡に達したときには極小になるという性質をもった特性関数であるから、化学反応が進むかどうかを判断する化学親和力の目安となる。
G=H-TS
で定義され、熱力学的ポテンシャルまたは定圧自由エネルギーともよばれる(Hは熱含量)。また一定温度、一定容積下での反応系ではヘルムホルツの自由エネルギーFが、原系から生成系へと自然に反応が進む場合にはしだいに減少し、平衡に達したときには極小になる。
[戸田源治郎]
『渡辺啓著『エントロピーから化学ポテンシャルまで』(1997・裳華房)』
改訂新版 世界大百科事典 「自由エネルギー」の意味・わかりやすい解説
自由エネルギー (じゆうエネルギー)
free energy
物質の熱力学的な性質を規定する関数(状態量)の一つ。ヘルムホルツの自由エネルギーとギブズの自由エネルギーの2種類があり,一般に系の変化は自由エネルギーの減少する方向にのみ進み,熱平衡状態はこれが極小となるとき実現する。
ヘルムホルツの自由エネルギー
ヘルムホルツの自由エネルギーFは,内部エネルギーU,エントロピーS,絶対温度Tを用いて,F=U-TSによって定義される。外部に対して仕事をするとき,熱の出入りがなければ,その仕事は内部エネルギーの減少分に等しいが,実際には熱の出入りが伴い,温度一定の下で仕事をする場合には,外部に仕事をすることによって下がる温度を補うため,外部から熱が流入する。このため,実際の仕事は内部エネルギーの減少分よりも少なくなる。前記の式をU=F+TSと書くと,Fは内部エネルギーのうち,仕事に変えられる部分という意味があることがわかり,閉じた系の等温変化では,それが可逆変化であれば外部に対してする仕事はFの減少分に等しい(不可逆変化ではこれより小さくなる)。自由エネルギーの名も,仕事に変えられるという意味からH.ヘルムホルツがつけた(1882)ものである。TSの部分は,系の乱れの度合を表す項で,いわば縛りつけられたエネルギーを表すことから,R.クラウジウスはこれを縛束エネルギーと呼んだ。閉じた系の等温等積での熱平衡条件は,F=極小で与えられる。
ギブズの自由エネルギー
ギブズの自由エネルギーGは,圧力p,体積Vを用いて,G=F+pV=H-TSで定義される(ただしHはエンタルピーで,H=U+pVである)。J.W.ギブズによって導入された。Gはヘルムホルツの自由エネルギーFをルジャンドル変換したもので,圧力を一定にしたとき,内部エネルギーのうち,仕事に変えられる部分を表す。したがって,閉じた系の等温等圧での熱平衡条件は,G=極小で与えられる。
執筆者:鈴木 増雄
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
化学辞典 第2版 「自由エネルギー」の解説
自由エネルギー
ジユウエネルギ
free energy
自由エネルギーにはヘルムホルツ(自由)エネルギー(記号A)とギブズ(自由)エネルギー(記号G)の二つがあり,
A = U - TS
G = H - TS
で定義される.Uは内部エネルギー,Hはエンタルピー,Sはエントロピー,Tは絶対温度.一定温度Tにおける系の変化に対する両者の変化は,
ΔA = ΔU - T(ΔS)
ΔG = ΔH - T(ΔS)
となる.自由エネルギーは物理化学の平衡論(相平衡および化学平衡)でもっとも重要な熱力学的関数であって,この概念を用いて多くの基本的法則(平衡定数,相律など)が導かれる.一定温度,一定圧力での系の自発的変化はΔG < 0の方向に起こる.したがって,平衡状態ではGは極小であり,系の微小変化に対しdG = 0.たとえば,反応物質と生成物質との間の化学平衡において,反応を一方向に微小量進行させても全系のGは不変であり,左辺と右辺のGは等しい.一定温度,一定蒸気圧下で平衡にある純液体とその飽和蒸気の系において,液体から飽和蒸気へ有限の変化を行った場合はΔG = 0,すなわち,このとき平衡にある二つの相での同量の物質のGは等しい.[別用語参照]化学ポテンシャル
出典 森北出版「化学辞典(第2版)」化学辞典 第2版について 情報
百科事典マイペディア 「自由エネルギー」の意味・わかりやすい解説
自由エネルギー【じゆうエネルギー】
→関連項目熱力学
出典 株式会社平凡社百科事典マイペディアについて 情報
ブリタニカ国際大百科事典 小項目事典 「自由エネルギー」の意味・わかりやすい解説
自由エネルギー
じゆうエネルギー
free energy
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
最新 地学事典 「自由エネルギー」の解説
じゆうエネルギー
自由エネルギー
free energy
⇒ ギブスエネルギー
出典 平凡社「最新 地学事典」最新 地学事典について 情報
栄養・生化学辞典 「自由エネルギー」の解説
自由エネルギー
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...

