ロピタルの定理（読み）ろぴたるのていり（その他表記）L'Hospital's theorem

日本大百科全書(ニッポニカ)

ロピタルの定理
ろぴたるのていり
L'Hospital's theorem

たとえば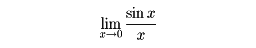

を考えるときx→0の極限においてはsinx/xは形として0/0になる。このような極限の形を不定形という。

　一般に、x→a（またはx→a+0,x→a-0,x→∞など）のとき、極限において0/0,∞/∞,0・∞,0⁰,∞⁰などの形となるものの極限値を、不定形の極限値という。

　ロピタルの定理は、このような極限値を求めるときに有効な定理で、次のようなものである。

　x→aのとき、f(x)/g(x)が0/0あるいは∞/∞の形の不定形であるとする。もしx=aを除いてf(x)/g(x)が微分可能で、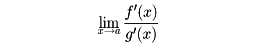

が存在するならば、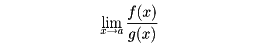

も存在して、この二つの極限値は相等しい。

　例1として次の式を考えてみる。

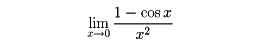
これは0/0形の不定形である。分子、分母を微分したものについて、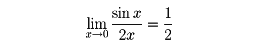

であるから、本題の極限は存在して、その極限値は1/2である。

　例2として次の式を考えてみる。

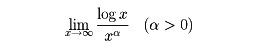
これは∞/∞形の不定形である。

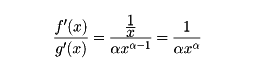
で、これはx→∞のとき0に収束する。本題の極限値は存在し、0に等しい。

［竹之内脩］

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

ロピタルの定理 (ロピタルのていり)
L'Hospital's theorem

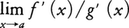関数f，gが閉区間［a，b］で連続，開区間（a，b）で微分可能，またg′（x）は（a，b）で0にならないとする。f（a）＝g（a）＝0であってが存在するならば，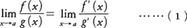

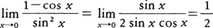
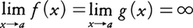すなわちf（a）/g（a）が0/0の形のとき，（1）の左辺の極限値の計算は分母，分子を別々に微分した右辺の極限値を計算すればよい。これをロピタルG.F.A.de L'Hospital（1661-1704）の定理，またはロピタルの法則という。例えば，

と求められる。f（a）/g（a）が∞/∞の形のときも同様な定理が成り立つ。すなわち，関数f，gが（a，b）において微分可能で，g′（x）は（a，b）で0にならないとき，かつ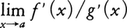が存在するならば（1）が成立する。この事実もロピタルの定理と呼ばれる。
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

世界大百科事典（旧版）内のロピタルの定理の言及

【微分】より

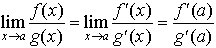…例えば，f,gがaの近傍で微分可能であってf(a)＝g(a)＝0であり，f′(x)/g′(x)がaで連続ならば，すなわち，f(a)/g(a)が0/0の形になるときには，上の極限値の計算は，分母，分子を別々に微分してx→aの極限値を計算すればよい。これをロピタルの定理という。例えば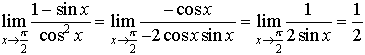，　f(x)が開区間Iでn回微分可能のとき，Iの中の点aを固定して，Iの任意の点xに対して，とおくと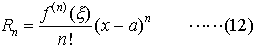，となるようなξがaとxとの間にある。…

※「ロピタルの定理」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」