日本大百科全書(ニッポニカ) 「分散分析法」の意味・わかりやすい解説
分散分析法
ぶんさんぶんせきほう
analysis of variance
分散分析法は、フィッシャーによって開発された方法で、農学実験に関する複雑な原因の分析に対して効果的に用いられた。この方法は広い範囲で応用されている。ここではもっとも簡単な場合の例として、この方法を平均の均一性の検定の問題に応用する。
r個の正規母集団をP1、P2、……、Prとし、Piの分布を平均値mi、分散σ2の正規分布N(mi,σ2)とする。ここでσ2は各Piについて同一であるが、その値は未知とする。
「r個のmiはすべて等しい」という仮説をHで表し、この仮説の検定を行う。
Piからの無作為抽出による標本を
{xi1,xi2,……,xini}
n=n1+n2+……+nr
と置く。ここで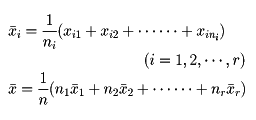
とし、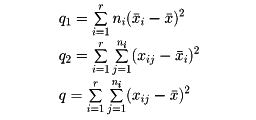
と置くと、qはq1とq2の和である(q=q1+q2)。qを総平方和という。
ここでXijは確率変数の実現値であるが、確率変数とみることにする。そうするとq1、q2、qも確率変数となる。このとき、次の定理が成り立つ。
「仮説Hの下では、q1とq2は独立であって、q/σ2,q1/σ2,q2/σ2の分布はそれぞれ自由度n-1,r-1,n-rのχ2分布である」。したがって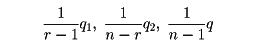
の平均値はどれもσ2に等しいことがわかる。また次の定理がある。
「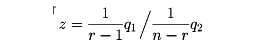
の分布は自由度r-1,n-1のF分布である」。
この定理に基づいて仮説Hの検定を行うことができる。すなわち、F分布の表を利用してzがλより大きい確率が0.01となるようなλを定めると、
z>λのとき仮説Hは捨てられ、
z≦λのとき仮説Hは捨てられない
ということになる。
分散分析法では、表(分散分析表)の形に整理しておくのが普通である。
[古屋 茂]


