双対性（読み）そうついせい

日本大百科全書(ニッポニカ)

双対性
そうついせい

数学用語の一つ。たとえば集合におけるド・モルガンの法則
　　(A∪B)′=A′∩B′,
　　(A∩B)′=A′∪B′
を考える。前の等式の∪、∩を入れ換えるならば後の等式を得る。この性質によって、集合の和と積についてのあらゆる定理は、∩と∪とを入れ換えることによってもう一つの定理が得られるという仕組みになっている。これを集合の和と積に関する双対性という。この双対性は、さらにさかのぼれば、論理における双対性にたどりつく。すなわちP、Qを命題とするとき
　　～(P∨Q)⇔～P∧～Q,
　　～(P∧Q)⇔～P∨～Q
であり、これが集合における双対性に対応する。さらには
　　～(∃x)P(x)⇔(∀x)～P(x),
　　～(∀x)P(x)⇔(∃x)～P(x)
という、全称記号∀と存在記号∃との双対性があって、集合においては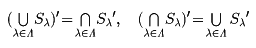

が対応している。ここで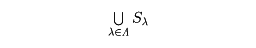

は、Λ=｛1,2,……｝のときS₁∪S₂∪S₃……となることを表す。

　数学においては基礎にこのような双対性があるために一種独特の整合性、対称性が生じているものと思われる。公理系が対称性をもっている理論ではつねに双対性が成り立つ。たとえば束(そく)の公理では二演算∪、∩に関して（∪、∩は集合の和、積とは限らない）、
　　a∪b=b∪a
　　(a∪b)∪c=a∪(b∪c),
　　(a∩b)∩c=a∩(b∩c)
　　(a∪b)∩a=a, (a∩b)∪a=a
という双対性があるため、束の定理ではつねに双対性が成り立つ。

　射影幾何学は平面と点とに関して双対的な公理系を有するため、点ということばと平面ということばを入れ換えれば双対的な定理が得られる。たとえば二次曲線に関するパスカルの定理はブリアンションの定理と双対である。

［足立恒雄］

[参照項目] | 射影幾何学 | 束

出典　小学館　日本大百科全書(ニッポニカ)

世界大百科事典（旧版）内の双対性の言及

【線形計画法】より

…はじめに実行可能基底解が得られていない場合に，人為的な変数を付加してから単体法を適用する二段階法や罰金法，はじめの係数に0が多い場合や条件や変数の数が多くてコンピューターの主記憶装置にすべての係数を格納できない場合に使える改訂単体法や積行列法など，単体法を発展させた解法がいくつか存在する。
［双対性］
　一つの線形計画問題が与えられたときに，その条件式の係数行列を転置して，もう一つの線形計画問題が作られる。この1対の問題の関係を双対性（そうついせい）dualityといい，元の問題を主問題，新たに作られた問題を双対問題という。…

【双対】より

…数学の理論において，いくつかの概念を二つずつ対応させるとき，定理が1対となって，そのおのおのは同じ構造をもつことがときどき起こる。この現象を双対性といい，対応する概念や定理を互いに他の双対という。例えば，平面射影幾何学で，“点”という概念と“直線”という概念を，“含む”という概念と“含まれる”という概念を対応させるとき，双対性がみられる。…

※「双対性」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」