精選版 日本国語大辞典 「射影幾何学」の意味・読み・例文・類語
しゃえい‐きかがく【射影幾何学】
- 〘 名詞 〙 射影と切断とを基本操作として図形の性質を研究する幾何学。
改訂新版 世界大百科事典 「射影幾何学」の意味・わかりやすい解説
射影幾何学 (しゃえいきかがく)
projective geometry
射影という対応によって不変に保たれる図形の性質(射影的性質)を主として研究する幾何学。その起源は,ユークリッド空間の射影的性質を研究した17世紀前半のG.デザルグやB.パスカルにあるが,射影空間上の幾何学として体系的に研究されて完成をみたのは19世紀前半である。19世紀後半にF.クラインにより,ユークリッド幾何学,非ユークリッド幾何学,アフィン幾何学などのいろいろな幾何学が射影幾何学から導きうることが示されるに及んで,射影幾何学は古典幾何学を統合するものとして,その重要性があらためて認識された。
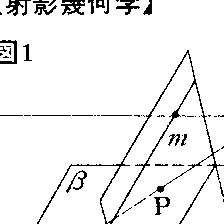
空間に2平面α,βとこれらの上にない1点Oが与えられたとき,α上の点Pを直線OPとβとの交点Qにうつす対応(中心射影)を考えよう。Oを通りβに平行な平面とαとの交線をmとするとき,Pがm上になければQは定まるが,Pがm上にあればQは存在しない。また,Oを通りαに平行な平面とβとの交線をnとするとき,Qがn上になければQにうつるPが定まるが,Qがn上にあればQにうつるPは存在しない(図1)。このような例外を解消するため次のように考える。空間の各直線lに対し,無限遠点と呼ぶ1点l∞を想像し,直線l,l′が平行ならばl∞=l′∞,そうでなければl∞≠l′∞と約束する。そして,平面αにその上の直線に対する無限遠点をすべてつけ加えて,これを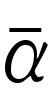 で表し,
で表し,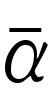 上にある無限遠点全体で一つの直線(無限遠直線)をつくると考える。このようにすれば,点Oからの中心射影で,m上の点は
上にある無限遠点全体で一つの直線(無限遠直線)をつくると考える。このようにすれば,点Oからの中心射影で,m上の点は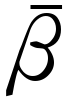 上の無限遠点にうつり,
上の無限遠点にうつり,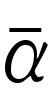 上の無限遠点はn上の点にうつって,
上の無限遠点はn上の点にうつって,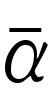 上の点と
上の点と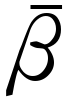 上の点が1対1に対応し,また
上の点が1対1に対応し,また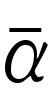 上の直線と
上の直線と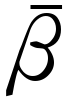 上の直線が1対1に対応する。
上の直線が1対1に対応する。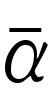 ,
,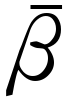 のように平面にその上の無限遠点をつけ加えたものを射影平面といい,上で述べた
のように平面にその上の無限遠点をつけ加えたものを射影平面といい,上で述べた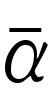 から
から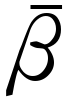 の上への1対1対応を点Oからの配景対応という。平面α,βとこれらに平行でない直線lが与えられたとき,α上の点Pに対し,その点を通りlに平行な直線がβと交わる点Qを対応させる対応(平行射影)を考えても,
の上への1対1対応を点Oからの配景対応という。平面α,βとこれらに平行でない直線lが与えられたとき,α上の点Pに対し,その点を通りlに平行な直線がβと交わる点Qを対応させる対応(平行射影)を考えても,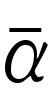 上の点,直線と
上の点,直線と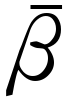 上の点,直線に関し上と同様のことがいえる。この
上の点,直線に関し上と同様のことがいえる。この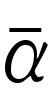 から
から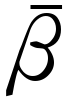 の上への1対1対応を無限遠点l∞からの配景対応という。いろいろな点からの配景対応を次々と有限回続けて行うことにより,最初の射影平面から最後の射影平面の上への1対1対応が得られるが,これを射影対応という。とくに一つの射影平面からそれ自身の上への射影対応を射影変換という。一つの射影平面上の射影変換の全体は群をつくる。射影対応で不変な性質を射影的性質というが,射影幾何学は図形のこのような性質を研究するもので,F.クラインの《エルランゲン・プログラム》流にいえば,(平面)射影幾何学は射影平面と射影変換群に属する幾何学となる。
の上への1対1対応を無限遠点l∞からの配景対応という。いろいろな点からの配景対応を次々と有限回続けて行うことにより,最初の射影平面から最後の射影平面の上への1対1対応が得られるが,これを射影対応という。とくに一つの射影平面からそれ自身の上への射影対応を射影変換という。一つの射影平面上の射影変換の全体は群をつくる。射影対応で不変な性質を射影的性質というが,射影幾何学は図形のこのような性質を研究するもので,F.クラインの《エルランゲン・プログラム》流にいえば,(平面)射影幾何学は射影平面と射影変換群に属する幾何学となる。
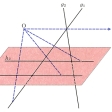
点Aが直線l上にあるということと,直線lが点Aを通るということとは同内容であるが,このことを点Aは直線lと結合しているという。結合性は射影的性質で,したがっていくつかの点が1直線と結合しているという性質(共線性)や,いくつかの直線が1点と結合しているという性質(共点性)は射影的性質である。そして,これらの性質のみを扱った定理,例えば次のデザルグの定理は射影幾何学の定理である。〈二つの三角形の対応する頂点を結ぶ3直線が共点ならば,対応する3辺の交点は共線である〉(図2)。ユークリッド幾何学のおもな対象である長さや角の大きさなどの計量的性質は射影的性質でなく,したがって三角形は射影幾何学の概念であるが,二等辺三角形や正三角形はそうではない。しかし数的な射影的性質もある。1直線l上に異なる4点A,B,C,Dがあるとき,l上に座標を導入してこれらの点の座標をx,y,u,vとすれば,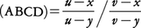 は座標のとり方によらない数で,4点A,B,C,Dの非調和比と呼ばれる。4点の中に無限遠点l∞があるときも,例えば(ABCl∞)=(u-x)/(u-y)のように定義される。射影対応で点A,B,C,Dに点A′,B′,C′,D′が対応すれば(ABCD)=(A′B′C′D′)が成り立ち,非調和比は射影的性質である。平面上に1点Oを通る4直線a,b,c,dがあるとき,Oを通らない直線lとこれらとの交点をA,B,C,Dとすれば,(ABCD)はlのとり方によらないので,これを(abcd)で表し,4直線a,b,c,dの非調和比という。平面上で1点Oを通るすべての直線の集合を直線束というが,二つの直線束の直線の間に1対1対応が与えられていて,直線a,b,c,dに対応する直線がa′,b′,c′,d′ならば,いつも(abcd)=(a′b′c′d′)が成り立つとき,これらの線束は射影的関係にあるという。射影的関係にある二つの線束において,対応する二つずつの直線の交点をつくれば,円,楕円,双曲線,放物線などの円錐曲線が得られる(図3)。このようなわけで,直線図形ばかりでなく,円錐曲線も射影幾何学の対象となる。これに関し,〈円錐曲線に内接する六角形の相対する辺の交わりである3点は共線である〉というパスカルの定理(図4),〈円錐曲線に外接する六角形の相対する頂点を結ぶ3直線は共点である〉というブリアンションの定理(図5)は有名である。射影平面上では,通常の平面上のときと同じく,〈異なる2点と結合する直線がつねに一つ定まる〉が,通常の平面上のときと違って平行線はなく,〈異なる2直線と結合する点がつねに一つ定まる〉。このように射影幾何学では点と直線の間に著しい類似性が見られ,このために射影幾何学の定理は二つずつ1対になっていて,そのおのおのは互いに類似している。例えばデザルグの定理とその逆,パスカルの定理とブリアンションの定理はそれぞれ1対となっている。この現象を射影幾何学の双対性という。
は座標のとり方によらない数で,4点A,B,C,Dの非調和比と呼ばれる。4点の中に無限遠点l∞があるときも,例えば(ABCl∞)=(u-x)/(u-y)のように定義される。射影対応で点A,B,C,Dに点A′,B′,C′,D′が対応すれば(ABCD)=(A′B′C′D′)が成り立ち,非調和比は射影的性質である。平面上に1点Oを通る4直線a,b,c,dがあるとき,Oを通らない直線lとこれらとの交点をA,B,C,Dとすれば,(ABCD)はlのとり方によらないので,これを(abcd)で表し,4直線a,b,c,dの非調和比という。平面上で1点Oを通るすべての直線の集合を直線束というが,二つの直線束の直線の間に1対1対応が与えられていて,直線a,b,c,dに対応する直線がa′,b′,c′,d′ならば,いつも(abcd)=(a′b′c′d′)が成り立つとき,これらの線束は射影的関係にあるという。射影的関係にある二つの線束において,対応する二つずつの直線の交点をつくれば,円,楕円,双曲線,放物線などの円錐曲線が得られる(図3)。このようなわけで,直線図形ばかりでなく,円錐曲線も射影幾何学の対象となる。これに関し,〈円錐曲線に内接する六角形の相対する辺の交わりである3点は共線である〉というパスカルの定理(図4),〈円錐曲線に外接する六角形の相対する頂点を結ぶ3直線は共点である〉というブリアンションの定理(図5)は有名である。射影平面上では,通常の平面上のときと同じく,〈異なる2点と結合する直線がつねに一つ定まる〉が,通常の平面上のときと違って平行線はなく,〈異なる2直線と結合する点がつねに一つ定まる〉。このように射影幾何学では点と直線の間に著しい類似性が見られ,このために射影幾何学の定理は二つずつ1対になっていて,そのおのおのは互いに類似している。例えばデザルグの定理とその逆,パスカルの定理とブリアンションの定理はそれぞれ1対となっている。この現象を射影幾何学の双対性という。
執筆者:中岡 稔
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「射影幾何学」の意味・わかりやすい解説
射影幾何学
しゃえいきかがく
projective geometry
射影対応(射影変換)によって不変な図形の性質を研究する幾何学である。たとえば、「いくつかの点が同一直線(または平面)上にある」は射影的に不変な性質である。一方、のように、交わる2直線g1、g2を点Oから射影し平面πで切断すれば、平行2直線h1、h2が得られるので、「平行」は不変な性質ではない。線分の長さ、角も不変ではないから射影幾何学では意味をもたない。もっとも簡単な射影的不変量は4点および4直線の非調和比で、これらは射影幾何学で基本的役割を果たすものである。射影対応で互いに移りうる図形を射影的合同といい、この合同概念はユークリッド幾何学での普通の合同に対応する役目をする。射影対応を特殊化したアフィン対応によってアフィン幾何学が構成される。ユークリッド幾何学は、アフィン対応をさらに特殊化した対応、すなわち、ユークリッド的合同変換で不変な図形の性質を研究する幾何学とみることができる。非ユークリッド幾何学も同様に構成されるので、射影幾何学はこれらすべてを包含する、より一般的な幾何学である。
射影幾何学はまた公理論的にもっともすっきりした美しい数学の一つで、ユークリッド幾何学に比べてはるかに少なく簡明な公理から出発し、厳密な論証によって幾何学を展開することができる。とくに射影幾何学では次に述べるように完全な双対(そうつい)性が成り立つことが著しい特徴である。いま、「2点を通る直線はちょうど一つ存在する」という命題を考えてみよう。この命題において、「点」↔「直線」、「を通る」↔「の上にある」の置き換えをしてみれば、「2直線の上にある点はちょうど一つ存在する」となる。このような置き換えによって、一つの命題から新しい命題をつくることを双対とよぶ。射影幾何学の公理系はそのどの公理の双対もまたこの公理系のなかに存在している。したがって、一つの命題が真ならばその双対命題は改めて証明しなくても必然的に真となる。ユークリッド幾何学の公理系はこのようにはなっていない。射影幾何学のおこりはルネサンス期の遠近画法であるといわれるが、今日の射影幾何学の端緒を開いたのはフランスの建築技術者デザルグである。パスカルはデザルグの仕事に刺激されて、今日パスカルの定理とよばれる定理をはじめとして円錐(えんすい)曲線に関する多くの射影幾何学的性質を発見した。その後、フランスの工兵士官ポンスレはナポレオンのロシア遠征に参加して捕虜となったが、獄中での研究をもとに双対の原理をみいだした。
[立花俊一]
百科事典マイペディア 「射影幾何学」の意味・わかりやすい解説
射影幾何学【しゃえいきかがく】
→関連項目幾何学|双対の原理|デザルグ|プリュッカー|ポンスレ
出典 株式会社平凡社百科事典マイペディアについて 情報
ブリタニカ国際大百科事典 小項目事典 「射影幾何学」の意味・わかりやすい解説
射影幾何学
しゃえいきかがく
projective geometry
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
世界大百科事典(旧版)内の射影幾何学の言及
【幾何学】より
…解析幾何学に対し,ユークリッド流に図形を直接考察する幾何学を総合幾何学,または純粋幾何学という。
[射影幾何学]
ルネサンス期のレオナルド・ダ・ビンチやA.デューラーのような芸術家たちによって始められた透視図法(遠近法)は,その後も技術的立場から研究され,17世紀には幾何学のこの方法による研究がG.デザルグやB.パスカルによって始められた。透視図法は空間の図形を1定点から射影して平面上に投影し,この投影図によって原図形を表現するという方法で,まさに写真による表現法である。…
【シュタイナー】より
…1834年ベルリン大学教授に就任,終生この職にとどまった。彼の最大の業績は当時フランスで新興した射影幾何学を継承して,それを総合的方法(数によらず図形そのものを直接考察する研究方法)によって発展させ,射影幾何学の基礎を築き上げたことである。そのほか,彼は初等幾何学における作図問題や最大・最小の問題に関して不滅の業績を残している。…
【デザルグ】より
…透視図法を研究するうち,幾何図形,とくに円錐曲線の性質が射影と切断によって統一的に導けることを発見し,1639年にこれに関する著書を刊行した。これには無限遠点,無限遠直線,極と極線,対合などの概念が述べられていて,この書は射影幾何学の起源とされている。二つの三角形に関する有名なデザルグの定理もこの中で述べられている。…
【パスカル】より
…早く妻を亡くしたエティエンヌは,1631年官を辞して一家でパリに赴き,メルセンヌの主宰する科学アカデミーに出入りするかたわら,子どもの教育に専念する。息子のパスカルは早熟の天才でとくに数学に才覚をあらわし,早くから父とともに科学者の集りに出席したが,16歳のときにデザルグの影響の濃い《円錐曲線試論》を発表(1640)し,射影幾何学における〈パスカルの定理〉を明らかにした。40年再び官についたエティエンヌとともに一家はルーアンに移る。…
※「射影幾何学」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...