公理（読み）コウリ

デジタル大辞泉

こう‐り【公理】

１ 一般に通用する道理。
２ 数学で、論証がなくても自明の真理として承認され、他の命題の前提となる根本命題。
３ 自明であると否とを問わず、ある理論の前提となる仮定。
[類語]論理・理り・理ことわり・道理・事理・条理・純理・理法・ロジック・理論・セオリー・原理・プリンシプル・定理

出典　小学館

精選版 日本国語大辞典

こう‐り【公理】

1. 〘 名詞 〙
2. ① 一般に通用する道理。社会を通して行なわれるはずの道理。公道(こうどう)。
   1. [初出の実例]「就之公理御越度には罷成間敷候哉」(出典：上杉家文書‐永正一六年（1519）一二月二一日・長尾景行書状)
   2. 「戦後」(出典：<出典>もはや)
   3. [その他の文献]〔呉志‐張温伝〕
3. ② 論理学で、演繹(えんえき)的理論の出発点として、証明なしに採用される命題。古くは、自明の理と考えられるものだけがそれに値するとされたが、現在では、その無矛盾性を証明することは不可能であっても、直接に自明の理として承認され、それによって他の命題を証明することのできる基本命題をいう。〔教育・心理・論理術語詳解（1885）〕

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

公理
こうり
axiom 英語
axiome フランス語
Axiom ドイツ語

ある理論の出発点となる仮定を公理という。数学における各理論は、いくつかの命題を前提とし、それらのみを仮定として展開される。すなわち、最初に仮定された命題や、それらからすでに導かれている命題を前提として、次々に新しい命題が導かれるのである。この仮定される最初の前提が、その理論の公理（あるいは公理系）とよばれるものである。

　そのような例としては、たとえば、自然数論の公理系として有名なペアノの公理がある。次の(1)～(5)がそれである。

(1)1は自然数である。

(2)nが自然数ならばn＋1も自然数である。

(3)nが自然数ならばn＋1≠1である。

(4)n＋1＝m＋1ならばn＝mである。

(5)自然数xについての述語P(x)について、P(1)および「任意の自然数kについてP(k)ならばP(k＋1)」が成立すれば、すべての自然数nについてP(n)である。

　かつては、公理とは「自明な命題」のことと考えられていた。つまり、いくつかの「自明な命題」から自明でない正しい命題を導き出すものが理論である、と考えられていたのである。紀元前300年ごろ集大成されたといわれているユークリッドの『幾何学原本』（ストイケイア）では、すでに、幾何学がこのように公理的に構成されている。そこでは、「任意の点から任意の点まで直線が引ける」などの公理からなっているが、そのなかには「平行線公理」といわれるものも含んでいる。この公理は他に比べて複雑で、あまり自明とも思われなかったため、他の諸公理から導けるものと考えられていたが、19世紀に至って、平行線公理のかわりに、その否定命題を公理としても新しい幾何学ができることが確かめられた。これが非ユークリッド幾何学である。

　公理とは「自明な命題」ではなく「理論の前提となる仮定」であるという認識は、このような歴史的展開から得られたのである。

［廣瀬　健］

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

公理【こうり】

古くはユークリッドの《幾何学原本》の初めにある〈共通概念〉（1.同じものに等しいものは互いに等しい，2.等しいものに等しいものを加えたものは互いに等しい，3.等しいものから等しいものを引いたものは互いに等しい，4.互いに重なり合う二つのものは等しい，5.全体は部分より大きい）またはこれと公準とを合わせて公理といい，幾何学構成の前提となる自明な命題と考えられた。しかし非ユークリッド幾何学の成立以来公理の性格について反省が加えられ，現在の数学では単に一つの理論の基礎として仮定する命題をその理論の公理という。このような公理から出発し論理に従い厳密な理論体系を建設すべきであるというのが公理主義の立場で，D.ヒルベルトにより主張され，現代数学を支配する根本思想となっている。→平行線公理
→関連項目数学｜ユークリッド幾何学

出典　株式会社平凡社

改訂新版　世界大百科事典

公理 (こうり)
axiom

数学や論理学における各理論は，いくつかの命題を前提とし，それらだけを用いて理論が展開される。その前提とする各命題がその理論の公理であり，前提とするいくつかの命題を併せたものが公理系である。採用する公理系を変えれば理論が証明する定理にも変化が起こる。ふつうの幾何学の公理系によるユークリッド幾何学に対し，平行線の公理の採用をやめて，次の（1），（2）の一方を採用した2種類の非ユークリッド幾何学の存在はその例である。（1）直線外の1点を通り，その直線と交わらない直線は少なくとも2本存在する。（2）直線外の1点を通り，この直線と交わらないような直線は存在しない。ユークリッドが公理および公準を導入したときは自明であるから証明なしで認めることにするというものから選んだのであるが，現代数学では理論の前提としての仮定という性格になっている。
執筆者：永田 雅宜

出典　株式会社平凡社「改訂新版　世界大百科事典」

普及版 字通

【公理】こうり

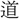公正の道理。〔管子、形勢解〕天を行ひ、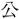理に出づれば、則ち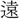き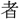も自ら親しみ、天を廢し、私爲を行はば、則ち子母も相ひ怨まん。

字通「公」の項目を見る。

出典　平凡社「普及版 字通」

ブリタニカ国際大百科事典 小項目事典

公理
こうり
axiom

数学の理論をつくるときの基礎におかれる命題で，無証明命題ともいわれる。公理という言葉は，ユークリッドの『原本』に述べられた公準および共通公理からきたものであるが，のちに，幾何学を構成する際の基礎におかれる命題の意味に使われるようになった。しかし，現在では，数学のあらゆる理論は，公理と呼ばれる基礎の命題から出発して，純粋に論理的に組立てられている。ある一つの理論の基礎におかれた公理全体を，公理系あるいは公理群という。初等幾何学における公理としては，点や直線や平面の基本性質のほか，平行線，結合，合同，順序，連続性などの基本的性質があげられる。また環や体の公理といえば，「加法の結合法則」をはじめ「乗法の結合法則」「分配法則」など演算の諸法則のうちのいくつかをさしていう。特に可換体は演算の諸法則の全部を公理系としている。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の公理の言及

【幾何学基礎論】より

…図形は直観的に認識されるものであるが，直観はしばしば客観性を欠くので，明確にいい表された定義や公理の上に，直観を排して厳正な証明によって一貫した論理体系としての幾何学を構成しようという思想である。《ストイケイア》は，まず点，直線，円などの定義definitionを述べ，続いて〈任意の2点は直線で結べる〉のような図形についての五つの基本性質を公準postulateとしてあげ，また〈同じものに等しいものは互いに相等しい〉のような量の相等についての九つの基本事項を公理axiomとしてあげる。そして，これらの定義，公準，公理より出発して順次に論理的推論によって，直観的知見を定理として導き出す。…

【公理系】より

…公理系とは，公理的体系の略称であって，とくに自然科学的学問を体系づける方法のひとつである。そのもっとも古い，しかも有名な例はユークリッド幾何学の体系であるが，20世紀に入って，いっそう明確な性格づけが与えられるようになった。その基本的な着想はつぎのようなものである。まず，一定の学問体系において基本的前提と考えられる命題の一定の組を選び出して，それらを公理axiomとよぶ。公理から一定の推理(推論)方法によって得られる結論を定理theoremとよぶ。…

【幾何学基礎論】より

…この著作は，古くから知られていた図形についての多くの知見を集大成して一つの学問体系にまとめあげたものであるが，これはプラトンによる次の思想の上に成立している。図形は直観的に認識されるものであるが，直観はしばしば客観性を欠くので，明確にいい表された定義や公理の上に，直観を排して厳正な証明によって一貫した論理体系としての幾何学を構成しようという思想である。《ストイケイア》は，まず点，直線，円などの定義definitionを述べ，続いて〈任意の2点は直線で結べる〉のような図形についての五つの基本性質を公準postulateとしてあげ，また〈同じものに等しいものは互いに相等しい〉のような量の相等についての九つの基本事項を公理axiomとしてあげる。…

【形式言語】より

…このシステムは記号論理の推論系を形式化したもので，3項組T＝(Σ，Ρ，α)で与えられる。ここに，αは公理といわれる一つの語，Ρはプロダクションと呼ばれる推論規則の集合，Σは公理とプロダクションに現れる文字の集合，つまりTのアルファベットである。実例を作ってみよう。…

【公理系】より

…公理系とは，公理的体系の略称であって，とくに自然科学的学問を体系づける方法のひとつである。そのもっとも古い，しかも有名な例はユークリッド幾何学の体系であるが，20世紀に入って，いっそう明確な性格づけが与えられるようになった。…

※「公理」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」