束（読み）ソク（英語表記）lattice

デジタル大辞泉

そく【束】［漢字項目］

［音］ソク（呉）　［訓］たば　つか　つかねる
［学習漢字］4年
〈ソク〉
１ 引き締めて一つにまとめる。「束帯・束髪／結束・収束」
２ 動きがとれないように引き締める。「束縛／検束・拘束・約束」
３ 一つにまとめたもの。たば。「幣束・維管束・二束三文」
〈たば〉「札束・花束」
［名のり］き・さと・つかぬ・つかね
［難読］束子たわし・不束ふつつか

つか【^▽束】

《「束つかねる」「掴つかむ」と同語源》
１ 梁はりの上や床下などに立てる短い柱。束柱つかばしら。
２ 紙をたばねたものの厚み。また、製本したときの本の厚み。「束が出る」「束見本」
３ 古代の長さの単位。指4本分の幅を基本とする、矢の長さをいうときに、八束やつか・十束とつかなどと用いる。
４ 古代、稲の量の単位。重さ1斤の稲を1把とし、10把を1束とした。

たば【束／^▽把】

［名］物をひとまとめにしてくくったもの。「薪を―にする」
［接尾］助数詞。たばねたものを数えるのに用いる。「花二―」「ねぎ一―」
[類語]房

そく【束】

１ 束ねたものを数える単位。稲など、10把をひとまとまりとしたもの。また、半紙10帖、すなわち200枚を1束という。「薪まき五束」
２ 矢の長さを測る単位。親指を除いた4本の指の幅を1束という。
「大矢と申す定の物の、十五―におとってひくは候はず」〈平家・五〉

出典　小学館

精選版 日本国語大辞典

そく【束】

1. 〘 名詞 〙
2. [ 一 ] 物を数える単位。
   1. ① 稲など一〇把をひとまとまりとしたもの。
      1. [初出の実例]「十段為_レ町。〈段祖稲二束二把。町祖稲廿二束〉」(出典：令義解（718）田)
   2. ② 半紙一〇帖、すなわち二〇〇枚をいう。
      1. [初出の実例]「有_二使者_一。吉野雑紙〈五束〉送_レ之」(出典：実隆公記‐大永七年（1527）七月六日)
   3. ③ 矢の長さをはかる単位。親指を除いた四本の指の幅。一にぎり分の長さ。約二寸五分（約七・七センチメートル）。
      1. [初出の実例]「君は実盛を大矢とおぼしめし候歟。わづかに十三束こそ仕候へ。〈略〉大矢と申ぢゃうの物の、十五束におとってひくは候はず」(出典：平家物語（１３Ｃ前）五)
   4. ④ 射芸で、蟇目(ひきめ)の矢二〇本のこと。〔岡本記（1544）〕
   5. ⑤ 薪炭、竹材などの容積にいう。
      1. [初出の実例]「薪を千束積て」(出典：清原国賢書写本荘子抄（1530）三)
   6. ⑥ 板、貫、小割などの木材の材積単位。四分板は二・五坪分、六分板では一・五坪分。
   7. ⑦ 釣りで、一〇〇尾をいう。「ハゼ五束」
3. [ 二 ] 江戸時代、商人などが用いた一、十、百、千などの数をいう符牒。
   1. ① 一をさす。
      1. [初出の実例]「一 そく よそともいふ」(出典：随筆・摂陽落穂集（1808）四)
   2. ② 十をさす。
      1. [初出の実例]「飯櫃の代りになる。蓋なしおかわ何ぼ何ぼ何ぼ。十五匁(ソクがれん)十五匁(ソクがれん)」(出典：浄瑠璃・いろは蔵三組盃（1773）七)
   3. ③ 百をさす。多く、寄席などの客の数についていう。
      1. [初出の実例]「買にゆく今ではしっかいそくでやす」(出典：雑俳・削かけ（1713）)
   4. ④ 千をさす。多く、金銭の一〇〇〇文すなわち一貫をいう。
      1. [初出の実例]「『鰹はそくろんじさ』『〈略〉いか程の事じゃ』『アイそくは一貫の事、ろんじはしれやせう』」(出典：咄本・無事志有意（1798）松魚)
4. [ 三 ]
   1. ① 約束のこと。主に、京都祇園の花街で、日柄約束の意に用いる。
      1. [初出の実例]「まづやかたへは、束(ソク)十ばかりを通して、生の五両は内証にして」(出典：洒落本・箱まくら（1822）上)
   2. ② 髪などをたばねること。
      1. [初出の実例]「なにを入れているのか髪の毛を束(ソク)に上へつっ立てて」(出典：巷談本牧亭（1964）〈安藤鶴夫〉春高楼の…)
   3. ③ 数学で、代数系の一つ。ある集合の上に二つの演算が定義され、それらが交換、結合の両法則をみたし、かつ互いに他に対する吸収法則をみたすならば、この集合を束という。

つか【束】

1. 〘 名詞 〙 ( 「つかねる（束）」「つかむ（掴）」と同源 )
2. ① 長さの単位。手でつかんだほどの長さ。すなわち、指四本分の幅にあたる。古代の単位で和数詞について「八束(やつか)」「十束(とつか)」などと用いる。後世は、矢の長さの場合だけに用いる。ただし、音読して「そく」という。
3. ② 古代、稲の量をはかるのに用いた単位。重さ一斤の稲を一把とし、一〇把を一束という。
   1. [初出の実例]「段(きた)ことに租(たちから)の稲、二束(ツカ)二把(たはり)」(出典：日本書紀（720）大化二年正月（北野本訓）)
4. ③ 紙をたばねたものの厚み。転じて、本の表紙を除いた中身の厚さ。書物の厚さ。〔現代語大辞典（1932）〕
5. ④ 「つかばしら（束柱）」の略。〔日葡辞書（1603‐04）〕

たばね【束】

1. 〘 名詞 〙 ( 動詞「たばねる（束）」の連用形の名詞化 )
2. ① 束ねること。束にすること。また、そのもの。たば。
   1. [初出の実例]「春の田をことありがほにかへせどもうてる蕨はたばねだになし〈源国信〉」(出典：堀河院御時百首和歌（1105‐06頃）春)
3. ② 取り締まること。ひとつにまとめること。また、その役やその人。取締役。監督。責任者。
   1. [初出の実例]「去程に帯と云は、物のたばねだぞ」(出典：松ヶ岡本人天眼目抄（1471‐73）上)
   2. 「此の心清町一町のたばねをする年寄」(出典：浄瑠璃・博多小女郎波枕（1718）中)
4. ③ 江戸時代に行なわれた、男の髪の結い方の一種。
   1. [初出の実例]「たばねを結ふ中にも、あの位(くれへ)手の利いた者は覚えねへ」(出典：滑稽本・浮世風呂（1809‐13）四)

たば【束・把】

1. [ 1 ] 〘 名詞 〙
   1. ① いくつかの物を一まとめにしてくくったもの。たばね。たばり。そく。
      1. [初出の実例]「外に見るめもあらめのたば」(出典：浄瑠璃・心中宵庚申（1722）下)
      2. 「訳の分らないものが、いくら束(タバ)になったって仕様がない」(出典：道草（1915）〈夏目漱石〉九三)
   2. ② 「たばかぜ（束風）」の略。〔随筆・烹雑の記（1811）〕
2. [ 2 ] 〘 接尾語 〙 たばねた物を数えるのに用いる。
   1. [初出の実例]「一束に折るや其角が梅の花〈蕉雨〉」(出典：俳諧・発句題叢（1820‐23）春)

つかね【束】

1. 〘 名詞 〙 ( 動詞「つかねる（束）」の連用形の名詞化 ) 一つにまとめてくくること。また、そのもの。薪や藁などの束を数えるときにも用いる。
   1. [初出の実例]「純束 ツカネ」(出典：観智院本名義抄（1241）)
   2. 「かりおけるつかねのあゐのそこらあればあくまで染めん色ぞしらるる〈藤原知家〉」(出典：新撰六帖題和歌（1244頃）六)

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

束 (そく)
lattice

数学用語。バンドルbundleの訳語として束という言葉が使われることがあるが，それは〈ファイバーバンドル〉の項目を参照。ここではlatticeの訳語としての束について述べる。ある集合が二つの演算（通常∪，∩で表す）をもち，すなわち，任意の二元a，bに対しa∪b，a∩bがそれぞれ一意的に定まり，次の性質（1）～（3）をもつとき，その集合を束という。なお，a∪bをa，bの結び，a∩bをa，bの交わりという。

　（1）　a∪b＝b∪a

　　　a∩b＝b∩a　……交換法則

　（2）　（a∪b）∪c＝a∪（b∪c）

　　　（a∩b）∩c＝a∩（b∩c）　……結合法則

　（3）　a∪（b∩a）＝a

　　　a∩（b∪a）＝a……吸収法則

　ある集合Mの部分集合全体S（M）を考えれば，束の例になる。また，自然数全体の集合Nにおいて，a∪bはaとbの最大公約数，a∩bはaとbの最小公倍数と定めれば，束になる。一つの束Lにおいて，新しい演算∪，∩を，

　a∪b＝（もとの演算でのa∩b）

　a∩b＝（もとの演算でのa∪b）

と定めると，やはり束になる。このように∪と∩とをとりかえた束を，もとの束の双対という。すべての束について成り立つ等式があれば，その式の∪と∩とをとりかえた等式も正しい。例えば，次のべき等法則は上の（2）と（3）から得られるが，一方を得れば，他方はその双対としても得られる。

　a∩a＝a，a∪a＝a

　一つの束Mにおいて，順序≧を，a≧b⇔a∪b＝aで定義すれば順序集合になるので，束においてはこの意味での順序を考える。二つの元a，bの上限（最小上界），下限（最大下界）はa∪b，a∩bである。逆に，順序集合Nにおいて，任意の二元a，bの上限c，下限dがともに存在するとき，a∪b＝c，a∩b＝dと定義すれば束になる。したがって，束とは，この性質をもつ順序集合であると思ってもよい。

　一つの束Lの部分集合L′について，その任意の二元a，bの結びa∪b，交わりa∩bがつねにL′に属するならば，L′はLにおける演算によって束になる。このときL′はLの部分束であるという。束L_λ（λ∈Λ）の直積пL_λにおいて，∪，∩を成分ごとに定めると，すなわち，（……，x_λ，……）∪（……，y_λ，……）＝（……，x_λ∪y_λ，……），（……，x_λ，……）∩（……，y_λ，……）＝（……，xλ∩y_λ，……）とすると，пL_λも束になる。これを束としての直積と定める。

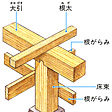
　束の有限個の元の関係を考えるのには，図のように大小関係のあるものは線で結び，大きいものは上方に位置するように図示するとわかりやすいことが多い。左の図の場合，a∪d＝a∪c，a∩c＝b∩dである。

　数学において，いろいろな束が現れるが，上の（1）～（3）以外の条件をさらに満たすことが多い。その条件に応じて，いろいろな名称が付されている。

モジュラー束

任意の三元a，b，cについて，モジュラー法則，すなわちa≦cならば，a∪（b∩c）＝（a∪b）∩cの成り立つ束をモジュラー束という。例えば，一つの群Gの正規部分群の全体N（G）において，a∪bは群としてのab＝｛xy｜x∈a，y∈b｝，a∩bは集合としてのa∩bと定めれば，モジュラー束になる。束がモジュラー束になるための必要十分条件は次のような関係にある三元a，b，cの存在しないことである。

　a＞c，a∪b＝c∪b，

　a∩b＝c∩b

　なお，上記のモジュラー法則は，a∪（b∩（c∪a））＝（a∪b）∩（c∪a）と同値であり，これをモジュラー法則ということもある。

相補束

束Lに最大元，最小元があるものとする。それらを1，0で表そう。Lの元aに対し，a∪b＝1かつa∩b＝0となる元bがあるとき，bはaの補元であるという。どの元にも補元があるとき，Lは相補束であるという。

分配束

任意の三元a，b，cに対して，

　a∩（b∪c）＝（a∩b）∪（a∩c）　……分配法則　

の成り立つ束を分配束という。上の等式は通常の分配法則の加法，乗法を∪，∩に変えた等式である。また，この条件は，

　a∪（b∩c）＝（a∪b）∩（a∪c）

と同値であるので，分配束の双対は分配束である。また，分配束は必ずモジュラー束であるが，モジュラー束は必ずしも分配束ではない。例えば，アーベル群Aによる，G＝A×Aの部分群のなすモジュラー束において，D＝｛（a，a）｜a∈A｝，B＝｛（a，1）｜a∈A｝，C＝｛（1，a）｜a∈A｝とおくと，D（B∩C）＝D，DB∩DC＝Gとなるからである。

ブール束

相補束であり，かつ分配束であるものをブール束または相補分配束という。ブール束においては，一つの元の補元は必ず一つだけである。一つの集合Mの部分集合全体S（M）はMを最大元，空集合を最小元とするブール束である。このとき補元は補集合である。また，S（M）の部分束Lで，〈XがLの元ならば，Xの補集合X^cもLに属する〉という条件を満たせば，Lもブール束になる。このようなLを集合ブール束と呼ぶ。どんなブール束も，束としての構造がそれと同じであるような集合ブール束が存在する。

完備束

束Lを順序集合と考えたとき，任意の空でない部分集合に上限および下限が必ず存在するとき，Lは完備であるという。上のS（M）は完備なブール束である。
→ブール代数

束群

群Gが束でもあり，次の条件が満たされるとき，Gは束群または束順序群であるという。

　a（b∪c）＝ab∪ac，（b∪c）a＝ba∪ca

　a（b∩c）＝ab∩ac，（b∩c）a＝ba∩ca

この条件はGを順序集合と考えたとき，

　a≦b　⇒　ac≦bc， ca≦cb

ということと同値である。

　束群Gにおいて，x＞1（単位元）であり，yが任意の元ならば，適当な自然数nをとれば，xⁿ＞yとなるとき，Gはアルキメデス的束群であるという。

　正の有理数全体Qにおいて，二元a，bをとったとき，それを通分して，m/d，n/dと表し，a∪b＝（mとnの最大公約数）/d，a∩b＝（mとnの最小公倍数）/dと定めると，a∪b，a∩bは通分のしかたにはかかわらず決まり，アルキメデス的束群になる。この束群においては，この束群の順序で1より大きい元全体（ふつうの大小で1より大きい自然数全体になる）が極小条件を満たす。そして，p＞1，かつp＞q＞1という元がないようなpが素数である。Qにおける素因数分解の一意性は，〈1より大きい元全体において極小条件が満たされる束群〉という観点から証明することができる。
執筆者：永田 雅宜

図－束

束 (そく)

（1）穫稲をはかる単位。収穫時に稲を束ねることに始まり，古くは〈つか〉ともよばれた。律令制下では10把を1束として籾1斗，米5升（後の2升強）となるのを標準とし，田租も稲束によって収納した。1束の稲を収穫しうる面積を1代（しろ）とよんだことから，50束を1反（段）とする面積単位となったこともある。近世でも束刈（そくかり）という面積単位が民間で行われている。律令制崩壊後は束の量は不定となり，江戸時代仙台地方の例では6把1束，1束から籾2～3升をとった。（2）以上のほか，束ねてまとめるものの単位として用い，〈たば〉ともよぶ。例えば杉原（すいばら）紙は20帖を束ねて1束とよんだ。（3）矢の長さを表す単位。指1本の幅を1伏（ぶせ）とし，4伏すなわち1握りの長さを1束とする。標準の矢は12束，およそ3尺前後である。《平家物語》に長い矢として，〈十五そく三伏〉の矢といった記事がある。
執筆者：歌川 学

出典　株式会社平凡社「改訂新版　世界大百科事典」

普及版 字通

束
常用漢字 7画

[字音] ソク
[字訓] つかねる・たばねる・たば

[説文解字]
[甲骨文]
[金文]

[字形] 象形
束薪の形。〔説文〕^六下に「るなり。口木に從ふ」とする。金文に「帛束」「絲束」「矢五束」などの語があり、一定数のものを束ねて一束とした。また束髪・束帯など、整えて結ぶことをいう。まとまることを結束といい、行動については終束という。

[訓義]
1. つかねる、たばねる、つかねたたば。
2. あつめる、あつめてむすぶ。
3. ちぢむ、せまい、しめる、つつしむ。

[古辞書の訓]
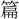〔名義抄〕束　ツカヌ・ツカム・トダル　〔立〕束　ツツム・サハク・シバル・チギル・ツカヌ・トトノフ・カタム・ツカサ・ユフ

[声系]
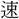〔説文〕に束声として（速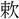）・など六字を収める。束声の字に、緊速の意をもつものが多い。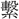

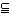[熟語]
束意▶・束躬▶・束錦▶・束▶・束検▶・束載▶・束矢▶・束手▶・束修▶・束脩▶・束装▶・束身▶・束紳▶・束薪▶・束芻▶・束素▶・束楚▶・束帯▶・束帛▶・束縛▶・束髪▶・束布▶・束脯▶・束腰▶・束聯▶
[下接語]
裹束・閣束・羈束・矜束・局束・窘束・結束・巻束・拘束・収束・集束・純束・装束・纏束・縛束・幣束・約束・要束・絡束・斂束

出典　平凡社「普及版 字通」

日本大百科全書(ニッポニカ)

束（数学）
そく
lattice

順序が定義されている集合Lがあって、Lの任意の二元a、bからなる集合｛a,b｝がつねに上限と下限をもつときLは束であるという。ここに、たとえばuが｛a,b｝の上限であるとは、uがLの元であってu≧a,u≧bが成り立ち、しかもx≧a,x≧bなるLの元xに対してはu≦xが成り立つことをいう。別のことばでいえば上限とは最小上界である。同様に、下限とは最大下界である。

［足立恒雄］

束の例

（1）一つの集合Mをとり、Mの部分集合の全体をLとする。Lの元a、bに対してab（aはbの部分集合）のときa≦bと定義する。この順序の定義によりLは束をなす。a、bをLの任意の二元とするとき、｛a,b｝の上限はa∪b（a、bの和集合）であり、下限はa∩b（a、bの共通部分）である。

（2）Nを自然数全体の集合とする。自然数aが自然数bを割り切るとき、a≦bと定義すると、Nはこの順序の定義により束をなす。任意の二つの自然数a、bに対して、｛a,b｝の上限はa、bの最小公倍数であり、下限は最大公約数である。

　束という概念は非常に幅の広い基本的な概念であって、いろいろな分野に登場する。

［足立恒雄］

束の基本性質

束Lにおいて｛a,b｝の上限を（集合の場合の類似で）a∪bで表し、下限をa∩bと表すことにすると、次の性質が成り立つ。

(1)べき等律　a∪a＝a, a∩a＝a
(2)交換律 　a∪b＝b∪a,
　　　　　　　a∩b＝b∩a
(3)結合律　(a∪b)∪c＝a∪(b∪c),
　　　 　　　 (a∩b)∩c＝a∩(b∩c)
(4)吸収律　(a∪b)∩a＝a,
　　　　　　　(a∩b)∪a＝a
　逆に、ある集合Lにおいて二つの演算∪、∩が定義されており、上記の交換律、結合律、吸収律の三法則が成り立てば、Lはa∪b＝bのときa≦bと定義することによって束となる。a∪b＝bはa∩b＝aと自然に同値となる。この束の定義からわかるように、Lにおけるある定理において∪と∩とを入れ換えれば、もう一つのLの定理が得られることは明らかで、この事実を双対性(そうついせい)という。射影幾何学の双対性は束の双対性として説明される。応用目的に応じて、種々の束がある。なかでも、完備束、ブール束（ブール代数）、モジュラー束など固有の深い研究がなされている。

［足立恒雄］

[参照項目] | 双対性

束（建築）
つか

短い柱。屋根を支える小屋組みや床を支えるために床下に使われる。日本では屋根には初め合掌あるいは扠首(さす)とよばれる斜材が使われ、束は用いられなかった。中国大陸から伝えられた仏教建築でも、束を使わない二重虹梁蟇股(こうりょうかえるまた)の構造が主流であった。束が目につく早い例には、法隆寺回廊の後補の部分や伊勢(いせ)神宮正殿妻の猪子(いのこ)扠首がある。伊勢神宮では内部に梁(はり)の上に立つ棟木を支える束が用いられている。1200年（正治2）ごろに大陸から入ってきた唐様(からよう)建築では、上部架構を支えるために梁の上に独特の形をした大瓶束(たいへいづか)を用いている。同じころやはり大陸から伝えられた天竺(てんじく)様でも、梁の上に円形断面の束が使われている。江戸時代に広く用いられるようになった和小屋では、棟木・母屋(おもや)を支えるのに束を用いるのが特徴である。床を支える床束(ゆかづか)は、弥生(やよい)時代の平出(ひらいで)遺跡（長野県）にすでに認められ、奈良時代には板敷きの普及に伴い広く用いられるようになったことが遺構から明らかである。

［平井　聖］

床束の構造

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

束
そく

(1) lattice　ラティスともいう。集合L の任意の元をx，y，z とし，この元の間に結合関係∪（結び）および∩（交わり）が定義されていて，次の条件が成り立つとき，集合L は束であるという。

(a) べき等律		x∪x＝x，x∩x＝x
(b) 交換律		x∩y＝y∩x，x∪y＝y∪x
(c) 結合律		（x∪y）∪z＝x∪（y∪z）
		（x∩y）∩z＝x∩（y∩z）
(d) 吸収律		（x∪y）∩x＝x
		（x∩y）∪x＝x

x∪y＝y のとき x≦y と考えて束は順序集合であり，逆に順序集合でx とy の上限，下限があるとき，それらを x∪y，x∩y とすれば束になる。全順序集合は，もちろん束になる。また，ある集合の部分集合の全体は束となるが，それは論理の束に対応していて，いわゆるブール束である。また，自然数も整除に関して，最大公約数と最小公倍数を考えれば束になる。
(2) bundle　ファイバー・バンドル（→ファイバー空間）のことをファィバー束と呼び，そのバンドル空間を束ということがある。区別するときには(1)をバーコフの束と呼ぶ。
(3) pencil　一点を通る直線または平面のなす図形。

出典　ブリタニカ国際大百科事典 小項目事典

リフォーム用語集

束

木造建築の構造部材の一種で、梁と棟木との間や、床下など、さまざまな部位に用いられる短い垂直の部材の事。束柱ともいう。床束、小屋束、釣束、えび束などがある。床束は、束石の上に立ち、床を支えている大引きを支える柱で、床にかかる荷重を地盤に伝えるもの。現在は腐食しないプラスチックや金属製のものもある。小屋束は、梁の上に垂直に立ち、母屋を受け支える柱の事を指す。

出典　リフォーム ホームプロ

山川 日本史小辞典 改訂新版

束
そく

穎稲(えいとう)をはかる単位。1束は10把に相当。1束を収穫する田の面積が1代(しろ)とされ，1束の稲は1斤の重さに相当し，穀1斗(米5升)に換算されるなど，他の単位の基準ともなった。田租の徴収，出挙稲(すいことう)の貸付なども束・把を単位として行われた(ただし田租は実際には穀で徴収)。中世～近世にも用いられたが，1束の量は不定となった。

出典　山川出版社「山川 日本史小辞典 改訂新版」

家とインテリアの用語がわかる辞典

つか【束】

建物の骨組みを構成する部材の一つ。短めの柱。小屋組みの梁(はり)と棟木(むなぎ)の間や床下などに用いる。◇「束柱(つかばしら)」ともいう。

出典　講談社

世界大百科事典（旧版）内の束の言及

【紙】より

…その他の紙についてもそれぞれの用途に応じて規定がある場合が多い。取引単位は，一般洋紙の場合は大口取引では連(1連＝1000枚)，小口取引では連，枚を，板紙の場合は大口取引では重量単位(t)，小口取引では束(1束＝25kg)，枚を用いる。紙の大きさには紙全紙の寸法と，書籍，雑誌，事務用紙などに仕上げた場合の寸法とがあり，前者を原紙寸法(または全紙寸法)，後者を紙加工仕上寸法という(表2，表3)。…

【はかり(秤)】より

…当時の史料をみると，穫稲の分量を測定する際，斗量の使用と同程度に〈斤〉を使用していたことが知られる。当時稲1束（そく）の重さを1斤とする史料があるが，これは1段250歩制に基づく穫稲1束の重量で，1段360歩制に基づく穫稲1束はこれよりも軽く，そこで前者を〈成斤（せいきん）〉と称するのに対し，後者を〈不成斤〉または〈小斤〉と称することがあった。この〈成斤〉1斤はメートル法に換算して，500～700gほどであることが確かめられている。…

※「束」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」