基本群（読み）きほんぐん（英語表記）fundamental group

改訂新版　世界大百科事典

基本群 (きほんぐん)
fundamental group

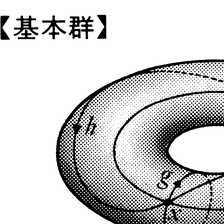
基本群は図形の位相的性質を代数的に研究するために，ホモロジー群とともに，H.ポアンカレによって導入された概念で，一次元ホモトピー群とも呼ばれる。これは図形Xとその1点xに対して定義され，π₁（X，x）で表される。xを出てxにもどるX上の閉曲線全体を考え，そしてxを動かさない連続的変形により互いにうつりうる閉曲線は同じ類にまとめる。この類がπ₁（X，x）の元で，閉曲線fの類と閉曲線gの類の積はfとgをつないだ閉曲線の類として定義される（図）。閉曲線fを逆向きに動いてできる閉曲線の類がfの類の逆元で，1点xを閉曲線とみたときの類がπ₁（X，x）の単位元である。図形Xが弧状連結ならばπ₁（X，x）はxのとり方によらずすべて同型となるので，この群をXの基本群といい，π₁（X）で表す。弧状連結な二つの図形が同相ならばそれらの基本群は同型である。基本群が単位元だけからなる連結な図形を単連結という。球面は単連結である。円周の基本群は整数のつくる加法群に同型である。二つの円周を1点で結んだ図形の基本群は可換群でない。基本群の概念を一般化して，n次元ホモトピー群π_n（X，x）が定義される。
執筆者：中岡 稔

図－基本群

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

基本群
きほんぐん

「ポアンカレ群」のページをご覧ください。

出典　ブリタニカ国際大百科事典 小項目事典