可換群（読み）カカングン（その他表記）commutative group

デジタル大辞泉

かかん‐ぐん〔カクワン‐〕【可換群】

元a、bが可換である群。アーベル群。

出典　小学館

改訂新版　世界大百科事典

可換群 (かかんぐん)
commutative group

群において，その演算が可換（乗法ならばab＝ba，加法ならばa＋b＝b＋aが，すべての2元a，bについて成立）であるとき，その群は可換群またはアーベル群Abelian groupであるという。N.H.アーベルが代数的に解ける方程式について研究した際に，ガロア群が可換群になるような拡大が扱われたので，この名があるという。

　0以外の有理数全体，0以外の実数全体，0以外の複素数全体などは，乗法に関して，可換群をなす。加法に関して可換群をなすものを，加群または加法群と呼ぶ。可換群の他の例としては，群Gの一つの元aで生成された群A（これを巡回群という。乗法の場合は，A＝｛aⁿ｜n＝0，±1，±2，……｝），群Gの中心（Gのどの元とも可換な元全体）などがある。

可換群の基本定理

有限個の元で生成された可換群は，有限個の巡回群の直積に分解する。

位数で可換性のきまる群

（1）p₁＜p₂＜……＜p_nが素数で，p_i－1がp_jの倍数ということが決しておきないときは，位数p₁p₂……p_nの群は巡回群に限る。例えば素数，3×5，3×11，5×17×19などである。

（2）p₁＜p₂＜……＜p_nが素数で，e_iが1または2p_i^ei－1がp_jの倍数ということが決しておきないとき，位数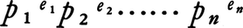の群は可換群に限る。例えば素数の平方，3²×5，3²×11，5²×17×19などである。
執筆者：永田 雅宜

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

可換群
かかんぐん

→アーベル群

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

可換群
かかんぐん

「アーベル群」のページをご覧ください。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の可換群の言及

【群】より

…　数の加法や乗法の場合には，条件(5)交換法則，すなわちa＊b＝b＊aが満たされている。このような場合，可換群またはアーベル群と呼ぶ。今後，この項では群の演算の記号は省略して，積はabのようにかく。…

※「可換群」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」