熱方程式（読み）ねつほうていしき

日本大百科全書(ニッポニカ)

熱方程式
ねつほうていしき

二階線形放物型偏微分方程式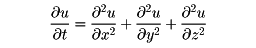

を熱方程式といい、均一な等方性媒質の熱伝導や粒子の拡散を記述する方程式として現れる。簡単のため空間一次元の場合の方程式

を考える。閉領域0≦t≦T,0≦x≦Lで連続な関数u(t,x)が0＜t≦T,0＜x＜Lで方程式（1）を満たすとき、その最大値、最小値は初期時刻t=0かまたは境界x=0,L上でとられる（最大値の原理）。このことから、たとえば境界条件u(t,0)=u(t,L)=0と初期条件u(0,x)=f(x)を満たす（1）の解はただ一つであることがわかる。ただし、f(x)は0≦x≦Lで連続で、両立条件f(0)=f(L)=0を満たすとする。さらにf(x)が0≦x≦Lで連続的微分可能ならば、この混合問題の解は変数分数形の解を重ね合わせて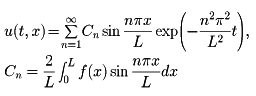

で与えられる。

　この解は0＜x＜L,t＞0で無限回微分可能で、一様収束の意味で初期関数f(x)に連続的に依存する。f(x)が-∞＜x＜∞で有界な連続関数のとき、初期条件u(0,x)=f(x)を満たす（1）のt＞0,-∞＜x＜∞で有界な解はただ一つ存在して

で与えられる。ただし初期条件は有界なxについて一様にu(t,x)→f(x)(t→0)であるという意味で満たされる。この解もt＞0,-∞＜x＜∞で無限回微分可能で、一様収束の意味で初期関数に連続的に依存する。空間多次元の場合も同様の事柄が成り立つ。

［小林良和］

出典　小学館　日本大百科全書(ニッポニカ)

世界大百科事典（旧版）内の熱方程式の言及

【数値解析】より

…数値解析の具体的な課題としては，問題の近似解を数値的に求めること，その近似解の性質，有効な数値計算の手順，真の値と近似解との理論的な差，丸めの誤差などの評価などである。以下では，数値解析の中の典型的な分野である，(1)行列の理論を含んだ線形代数の諸問題，(2)非線形方程式，とくに代数方程式の解法，(3)常微分方程式や熱方程式などの取扱いなどについて，考え方の例をみることにする。このほか数値積分や補間法などに現れる計算も重要な数値解析の話題になっている。…

※「熱方程式」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」