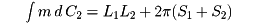積分幾何（読み）せきぶんきか

日本大百科全書(ニッポニカ)

積分幾何
せきぶんきか

積分幾何は、ブラシュケW. Blaschke、サンタロL. A. Santaloなどの学者によって始められた幾何学の一分野である。平面π上に直交座標系R₀を定めておく。π上の図形Fに対して、Fに固定した直交座標系Rを定め、Rの原点PのR₀に関する座標を(x,y)とし、Rのx軸がR₀のx軸となす角をθとして、dF=dPdθ=dxdydθによってFの位置密度を定める。この位置密度は座標系の選び方に無関係であり、またFに運動を施しても不変である。

［古屋　茂］

クロフトンの公式

xcosθ+ysinθ=pで表される直線と長さLの曲線Cとの交点の数をn(p,θ)とすると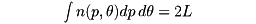

が成り立つ。これをクロフトンの公式という。次に、長さLの凸閉曲線Cが囲む面積をSとする。Cの外側の点PからCへの二つの接線のなす角をωとすると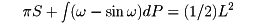

が成り立つ。この式もクロフトンの公式とよばれている。

［古屋　茂］

ポアンカレの公式

平面上の二つの曲線C₁、C₂の長さをそれぞれL₁、L₂とする。C₁を固定してC₂を移動させ、C₁とC₂の交点の数nを、C₁に交わるC₂のあらゆる位置について積分すると、その値は4L₁L₂となる。すなわち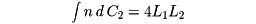

これをポアンカレの公式という。

［古屋　茂］

ブラシュケの基本公式

平面上の二つのジョルダン閉曲線をC₁、C₂とし、それぞれの長さをL₁、L₂、囲む面積をS₁、S₂とする。C₁を固定してC₂を移動させ、C₁、C₂の囲む領域の共通部分の連結領域の個数をmとすると、C₁に交わるC₂のあらゆる位置についてのmの積分について次の等式が成り立つ。

これをブラシュケの基本公式という。

　以上では平面の場合についていくつかの公式をあげたが、n次元ユークリッド空間における種々の図形の密度に関する公式が得られている。またさらに一般的な研究が進められている。

［古屋　茂］

出典　小学館　日本大百科全書(ニッポニカ)