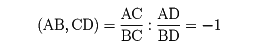調和列点（読み）ちょうわれってん

日本大百科全書(ニッポニカ)

調和列点
ちょうわれってん

一直線上の4点A、B、C、Dがあり、その非調和比が－1、すなわち

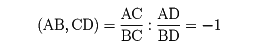
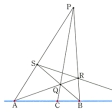
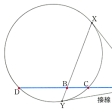
であるとき、この4点を調和列点（または調和点列）という。ここでACなどはA、C間の符号をもつ距離である。このとき、点C、DはA、Bを調和に分かつといい、CとDを互いの調和共役点という。非調和比について(AB,CD)=(CD,AB)の関係式が成り立つから、C、DがA、Bを調和に分ければ、A、BもC、Dを調和に分け、AとBも互いの調和共役点である。完全四角形（図A）を利用すれば、与えられた線分ABとその上の任意の点Cとに対して、Cの調和共役点Dを次のようにして求めることができる。直線AB上にない任意の点Pをとり、次に線分PC上に任意に点Qをとる。さらに点R、Sを図Aに従ってとれば、直線SRと直線ABとの交点Dが求める点である。調和列点の別の例は図BのA、B、C、Dである。ここでAは円外の任意の点、AX、AYは円の接線で、直線ADはAを通り線分XYと交わる任意の直線である。

［立花俊一］

[参照項目] | 非調和比

調和列点説明図〔図A〕

調和列点説明図〔図B〕

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

調和列点 (ちょうわれってん)
harmonic range

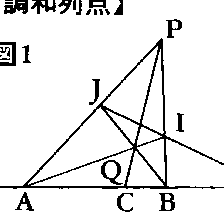
点C，Dにより線分ABが同じ比に内分および外分されているとき，4点A，B，C，Dは調和列点であるという。このとき，また，C，DはA，Bを調和に分かつともいい，CとDの一方をA，Bに関する他方の調和共役点という。A，B，C，Dが調和列点ならば，B，A，D，CおよびC，D，A，Bも調和列点である。1直線l上に3点A，B，Cがあるとき，点Pをlの外にとってPとA，B，Cを結び，次に点QをPC上にとって，AQとBPの交点をI，BQとAPの交点をJとし，IJとlとの交点をDとすれば，DはA，Bに関するCの調和共役点である（図1）。1点Oからでる4直線a，b，c，dとOを通らない1直線lとの交点A，B，C，Dが調和列点であるならば，Oを通らないどんな直線l′とa，b，c，dの交点A′，B′，C′，D′も調和列点である。このときa，b，c，dは調和線束であるという（図2）。A，B，C，Dが調和列点のとき，ABの中点をOとすればOA²＝OC・ODで，この逆も成り立つ。三角形ABCの角Cおよびその外角の2等分線が直線ABと交わる点をP，Qとすれば，A，B，P，Qは調和列点である（図3）。一つの円に円外の点Aからこの円と交わる直線lを引いて円周との交点をC，Dとし，またAからこの円に二つの接線を引いて接点を結ぶ直線mを作り，lとmとの交点をBとすれば，A，B，C，Dは調和列点である（図4）。
執筆者：中岡 稔

図1～図4

出典　株式会社平凡社「改訂新版　世界大百科事典」