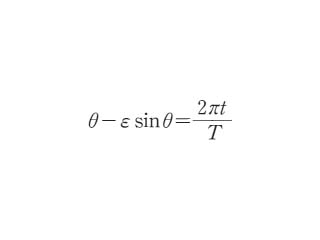改訂新版 世界大百科事典 「ケプラーの方程式」の意味・わかりやすい解説
ケプラーの方程式 (ケプラーのほうていしき)
Kepler's equation
ケプラー運動を行っている惑星の位置推算に現れる方程式。離心近点角をE,平均近点角をM,離心率をeとすると,これらの間に,E-e sin E=Mの関係があり,この関係はeとMを与えてEを求めるための超越方程式となっている。Mは近日点通過後の経過時間に比例する量であり,位置推算時刻が決まれば与えられる。ケプラーの方程式を解いてEを求めると,近日点から惑星までの角距離vは,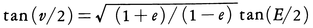 の関係によって求められるので惑星の軌道上の位置が決まる。ここにvは真近点角といわれる。ケプラーの方程式は,ケプラーが火星の運動の研究の途次に見いだしたもので,文献に現れた最古の超越方程式といわれる。これまでに何百という解法が考案されてきたことでも有名である。なお,放物線運動の場合には,ケプラーの方程式は三次方程式に帰着される。
の関係によって求められるので惑星の軌道上の位置が決まる。ここにvは真近点角といわれる。ケプラーの方程式は,ケプラーが火星の運動の研究の途次に見いだしたもので,文献に現れた最古の超越方程式といわれる。これまでに何百という解法が考案されてきたことでも有名である。なお,放物線運動の場合には,ケプラーの方程式は三次方程式に帰着される。
執筆者:堀 源一郎
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報