離心角（読み）りしんかく（英語表記）eccentric angle

改訂新版　世界大百科事典

離心角 (りしんかく)
eccentric angle

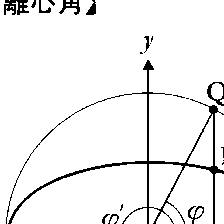
（1）楕円は，その中心を原点Oとしその長軸をx軸とする直交座標系を用いれば，（x/a）²＋（y/b）²＝1という形の方程式で表されるが，このとき円x²＋y²＝a²を楕円の補助円という。いま，楕円の周上に点Pがあるとき，Pを通ってx軸に垂直にひいた直線が補助円と交わる点のうちPと同じ象限にあるものをQとし，半直線OQがx軸の正の方向となす角をφとすれば，Pの座標（x，y）はx＝acosφ，y＝bsinφで表される。φを点Pの離心角という。（2）双曲線は，その中心を原点Oとし主軸をx軸とする直交座標系を用いれば，（x/a）²－（y/b）²＝1という形の方程式で表されるが，このとき円x²＋y²＝a²を双曲線の補助円という。いま，双曲線上に点Pがあるとき，Pからx軸に垂線を下ろしてその足から補助円に接線を引き，Pが第1，第2，第3，第4象限内にあるかに応じてそれぞれ第1，第3，第2，第4象限内の接点をQとし，半直線OQがx軸の正の方向となす角をφとすれば，Pの座標（x，y）はx＝asecφ，y＝btanφで与えられる。φを点Pの離心角という。（3）楕円の離心率をeとすれば0≦e＜1であるから，e＝sinφとなる鋭角φが定まる。このφを天文学では楕円軌道の離心角と呼ぶ。
執筆者：中岡 稔

図1～図2

出典　株式会社平凡社「改訂新版　世界大百科事典」

世界大百科事典（旧版）内の離心角の言及

【双曲線】より

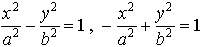…双曲線は媒介変数θを用いて，x＝asecθ,y＝btanθの形に表される(図3)。このθを双曲線上の点P(x,y)の離心角という。二つの双曲線，は互いに共役という(図2)。…

※「離心角」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」