テーラーの定理（読み）テーラーのていり（その他表記）Taylor's theorem

ブリタニカ国際大百科事典 小項目事典

テーラーの定理
テーラーのていり
Taylor's theorem

関数 y＝f(x) が閉区間 [a，a＋h] で連続で，この区間内で微分可能ならば，a と a＋h の間には等式 {f(a＋h)－f(a)}/h＝f'(a＋θh)(0＜θ＜1) ，または書き換えて f(a＋h)＝f(a)＋h・f'(a＋θh) を成り立たせるような θ が，少くとも1つ存在することが知られている (平均値の定理) 。これを拡張したものがテーラーの定理である。定理は次のように述べられる。関数 y＝f(x) が区間 [a，a＋h] で連続で，n 回微分可能，すなわち n 次までの導関数 f'(x)，f''(x)，…，f⁽ⁿ⁾(x) をもつならば，等式
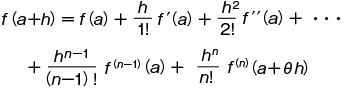が成立する 0＜θ＜1 である θ が存在する。これをテーラーの定理といい，上の等式の右辺をテーラーの展開式あるいはテーラーの公式という。また右辺の最後の項 f⁽ⁿ⁾(a＋θh)hⁿ/n!＝R_n を展開式の剰余項あるいは単に剰余という。他の剰余式と区別するときには，これをラグランジュの剰余形式という。テーラーの定理は，1つの関数 f(x＋h) を，そのテーラー展開式で表わされる整関数で近似した場合，そこに現れる剰余についての定理ということもできる。 f⁽ⁿ⁾ も連続なら，R_n は積分を使って
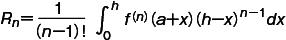と表わすこともでき，微分よりは積分のほうが扱いよいので，最近では積分型の剰余項を使うことが多い。

出典　ブリタニカ国際大百科事典 小項目事典