改訂新版 世界大百科事典 「フーリエ積分」の意味・わかりやすい解説
フーリエ積分 (フーリエせきぶん)
Fourier integral
(-∞,∞)において積分可能な関数f(x)に対して,次の関数F(t)を考える。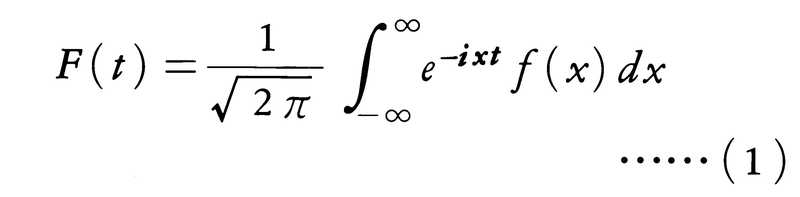
この右辺の積分をフーリエ積分といい,左辺の関数F(t)をf(x)のフーリエ変換という。また(1)によるfからFへの変換をもフーリエ変換という。これは有限区間における関数のフーリエ係数を求めることに相当する。有限区間で関数をフーリエ級数に展開することに対応して(-∞,∞)上の関数f(x)を,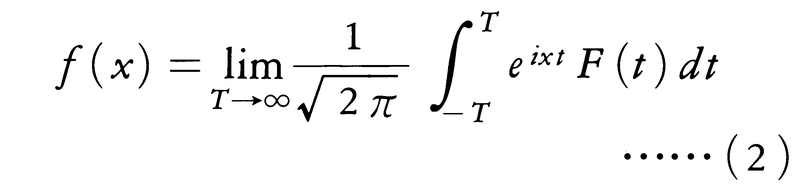
のような形に表すことを考える。f(x)が点xの近傍で有界変動ならば,(2)の左辺を1/2{f(x+0)+f(x-0)}で置き換えた式が成立する。とくにf(x)が実数値ならば(2)は,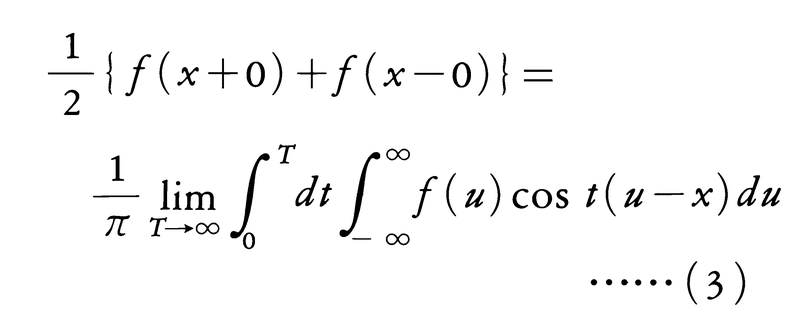
となり,これは次の式とも同等である。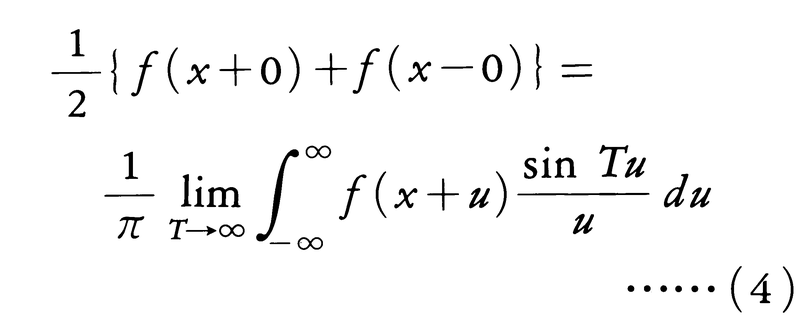
(3),(4)をそれぞれフーリエの二重積分定理,単積分定理という。fが(-∞,∞)で2乗可積分のときは,任意のa>0に対して,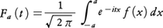 がtについて2乗可積分であって,
がtについて2乗可積分であって,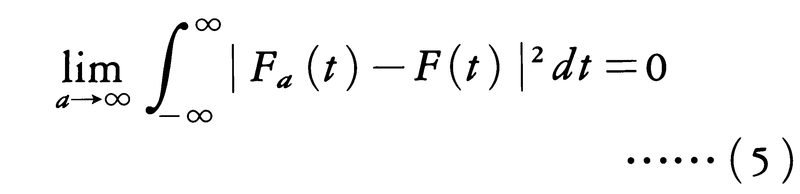
なる2乗可積分関数F(t)が存在する。(5)が成り立つとき,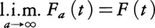 と書きFaがFに平均収束するという(記号l.i.m. はlimit in meanと読む)。このとき(2)は,
と書きFaがFに平均収束するという(記号l.i.m. はlimit in meanと読む)。このとき(2)は,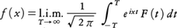 の意味で成立する。この事実をプランシュレルの定理という。さらにパーセバルの等式,
の意味で成立する。この事実をプランシュレルの定理という。さらにパーセバルの等式,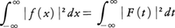 が成立する。fとその導関数f′が可積分のとき,fのフーリエ変換をF(t)とすると,f′のフーリエ変換は-itF(t)になる。
が成立する。fとその導関数f′が可積分のとき,fのフーリエ変換をF(t)とすると,f′のフーリエ変換は-itF(t)になる。
すなわち微分演算がフーリエ変換により単に-itを掛けることで置き換えられる。この事実は微分方程式の解法に応用される。
執筆者:伊藤 清三
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報

