モール円（読み）モールえん

最新 地学事典

モールえん
モール円

Mohrʼs circle

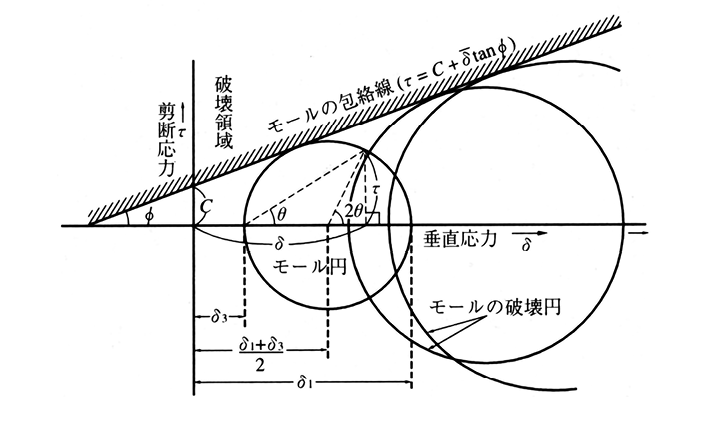
O.Mohrによる応力の一図解法。最大，最小主応力δ₁，δ_３が与えられているとき，任意の点を通る面上の垂直応力をδ，剪断応力をτとし，面の傾きをθとすれば，δ＝１/２（δ₁＋δ_３）＋１/２（δ₁─δ_３）cos２θ，τ＝１/２（δ₁─δ_３）sin２θで求まる。δを横軸に，τを縦軸にとり，主応力差（deviator stress）δ₁─δ_３を直径とするモール円を描き，δ_３の点よりδ軸とにθの角をなす直線を引き円との交点を求めると，その座標はθの傾きをなす面上のδとτの値となる。種々の応力状態で描いた破壊時のモール円（モールの破壊円）はいずれも一つの直線に接する。この線をモールの包絡線と呼ぶ。この線はクーロンの式τ＝C＋tanφ（C：粘着力，：有効応力，φ：内部摩擦角）で表され，クーロンの破壊線とも呼ばれる。この線の上側の応力域は破壊領域となる。

執筆者：桑原 徹

出典　平凡社「最新 地学事典」

改訂新版　世界大百科事典

モール円 (モールえん)

→粉粒体

出典　株式会社平凡社「改訂新版　世界大百科事典」

世界大百科事典（旧版）内のモール円の言及

【粉粒体】より

…粉粒体の内部における主応力をσ₁,σ₂とすれば，この円の上の任意の点Pのσ,τ座標値は，粉粒体内部の任意の面に対して作用する垂直応力とせん断応力の関係を満足している。このような円は粉粒体(あるいは一般に固体)の内部の応力状態を表しており，モールの応力円，またはモール円と呼ばれる。粉粒体が滑りを起こす限界応力状態に対応するモール円をいくつも描くと，その包絡線が得られる。…

※「モール円」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」