世界大百科事典(旧版)内のコッホ曲線の言及
【フラクタル】より
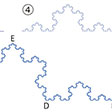
…もう一つの例はG.カントルの三進集合で,線分を3等分し,両端の二つの小線分を残すという操作を無限に行い,元の線分上に最後まで残っている点の集合である。さらに平面上の集合での簡単な自己相似図形はフォン・コッホH.von Kochが1906年に発見したコッホ曲線であって,その自己相似性は図を見れば明らかであろう。 マンデルブローB.B.Mandelbrotは1967年ころに今まで述べたような自己相似図形やそれに関連した自己相似性をもつ図形をフラクタルと名づけ,コンピューターはこのような自己相似性をきわめて精度よく表現しうることを利用して,きわめて美しいフラクタルの数々を発表している。…
※「コッホ曲線」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
〘 名詞 〙 春の季節がもうすぐそこまで来ていること。《 季語・冬 》 〔俳諧・俳諧四季部類(1780)〕[初出の実例]「盆栽の橙黄なり春隣〈守水老〉」(出典:春夏秋冬‐冬(1903)〈河東碧梧桐・高...