日本大百科全書(ニッポニカ) 「ヤコビアン」の意味・わかりやすい解説
ヤコビアン
やこびあん
Jacobian
関数行列式ともいう。数学者ヤコービの名をとってつけられた。多変数関数を扱う際に非常に重要な意味をもつ行列式である。ここでは二変数の場合について説明する。
二変数x、yの二つのC1級関数(偏導関数が存在して連続であるような関数)f(x,y),g(x,y)があるとき、次の行列式(*)によって定められる関数を、f、gのx、yに関するヤコビアンという。
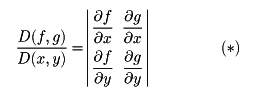
いま、u=f(x,y),v=g(x,y)によって、変数x、yを変数u、vに変換することを考える。このとき、1点(x0,y0)の十分小さな近傍では、この変換は線形変換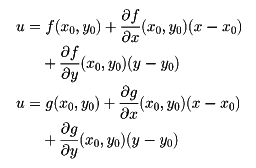
にほぼ等しく、ヤコビアンは、この線形変換の係数の行列式である。この意味でヤコビアンは、多変数関数の解析につねに登場し、中心的な役割を果たすものである。
[竹之内脩]
逆変換
変換u=f(x,y),v=g(x,y)があるとき、ある点(x0,y0)で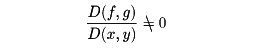
ならば、点(x0,y0)の近傍では、対応(x,y)→(u,v)は1対1となり、逆変換x= (u,v),y=ψ(u,v)が存在する。ここで、
(u,v),y=ψ(u,v)が存在する。ここで、 、ψはu、vのC1級関数である。
、ψはu、vのC1級関数である。
[竹之内脩]
陰関数定理
F(x,y,z),G(x,y,z)は三変数x、y、zのC1級関係であるとする。このとき、点(x0,y0,z0)において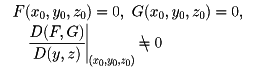
ならば、C1級関数f(x),g(x)が存在して、
f(x0)=y0, g(x0)=z0
かつ、x0の近傍でつねに
F(x,f(x),g(x))=0, G(x,f(x),g(x))=0
が成り立つ。すなわち
F(x,y,z)=0, G(x,y,z)=0
は、y、zに関して解ける。これを陰関数定理という。
[竹之内脩]


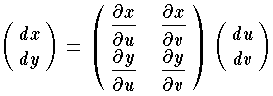 なので,この無限小変換の面積比にあたる行列式
なので,この無限小変換の面積比にあたる行列式 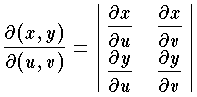 を,2つの関数 x ,y の u ,v に関するヤコビアンという。 x ,y の間に
を,2つの関数 x ,y の u ,v に関するヤコビアンという。 x ,y の間に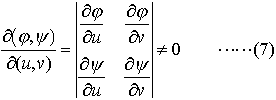 とすると,A,Bのうち一方が面積確定なら他方も面積確定で,
とすると,A,Bのうち一方が面積確定なら他方も面積確定で,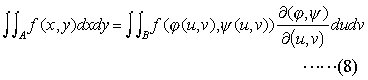 (7)の行列式を関数行列式,またはヤコビの行列式(ヤコビアンJacobian)という。とくに,x=rcosθ,y=rsinθ(二次元の極座標)とすると,
(7)の行列式を関数行列式,またはヤコビの行列式(ヤコビアンJacobian)という。とくに,x=rcosθ,y=rsinθ(二次元の極座標)とすると,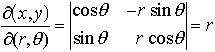 であるから,
であるから,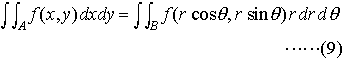 三次元の場合にはx=φ(u,v,w),y=ψ(u,v,w),z=χ(u,v,w)について上と同様な仮定のもとに,関数行列式,
三次元の場合にはx=φ(u,v,w),y=ψ(u,v,w),z=χ(u,v,w)について上と同様な仮定のもとに,関数行列式,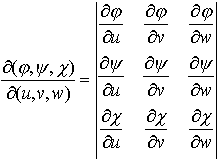 を用いて(8)と同様な公式を書くことができる。…
を用いて(8)と同様な公式を書くことができる。…