改訂新版 世界大百科事典 「ラテン方陣」の意味・わかりやすい解説
ラテン方陣 (ラテンほうじん)
Latin square
n行n列の正方形の格子にn種の記号をn個ずつ入れ,どの行,どの列にも,n種の記号が1個ずつ現れるようにしたものをラテン方陣またはラテン方格という。図1は三次と四次のラテン方陣の例である。n次のラテン方陣の個数をn!(n-1)!×inとすると,i1=i2=i3=1,i4=4,i5=56,i6=9408,i7=16942080,i8=535281401856となる。n!(n-1)!倍したのは,一つの標準方陣の行または列の入替えで,これだけの異なる方陣が得られるからである。n≧9のとき,inの正確な値は知られていないが,近似的には,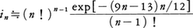 となる。n次のラテン方陣を2個重ねてn2通りのすべての記号の組合せが得られるとき,この2個の方陣は直交するといい,できた方陣をオイラー方陣またはグレコ・ラテン方格という。図2は三次と四次のオイラー方陣の例である。六次のオイラー方陣は存在しないが,それを除くと,三次以上のオイラー方陣はすべて存在する。図3は十次のオイラー方陣で,オイラー自身は存在しないと予想したのに,実際は存在したということで有名である。互いに直交するn次のラテン方陣の個数は,多くてもn-1個までで,nが素数かそのべき乗のときは,ちょうどn-1個の方陣が存在する。なお,互いに直交するラテン方陣は実験計画法の分野で有効に活用されるので,今日でも盛んに研究されている。
となる。n次のラテン方陣を2個重ねてn2通りのすべての記号の組合せが得られるとき,この2個の方陣は直交するといい,できた方陣をオイラー方陣またはグレコ・ラテン方格という。図2は三次と四次のオイラー方陣の例である。六次のオイラー方陣は存在しないが,それを除くと,三次以上のオイラー方陣はすべて存在する。図3は十次のオイラー方陣で,オイラー自身は存在しないと予想したのに,実際は存在したということで有名である。互いに直交するn次のラテン方陣の個数は,多くてもn-1個までで,nが素数かそのべき乗のときは,ちょうどn-1個の方陣が存在する。なお,互いに直交するラテン方陣は実験計画法の分野で有効に活用されるので,今日でも盛んに研究されている。
執筆者:中村 義作
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
百科事典マイペディア 「ラテン方陣」の意味・わかりやすい解説
ラテン方陣【ラテンほうじん】
出典 株式会社平凡社百科事典マイペディアについて 情報
ブリタニカ国際大百科事典 小項目事典 「ラテン方陣」の意味・わかりやすい解説
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...


