分数関数（読み）ブンスウカンスウ

デジタル大辞泉

ぶんすう‐かんすう〔‐クワンスウ〕【分数関数】

分数式で表される関数。

出典　小学館

日本大百科全書(ニッポニカ)

分数関数
ぶんすうかんすう

多項式の商の形で表された関数、つまり、g(x)およびh(x)を多項式とするとき、y=g(x)/h(x)の形で表される関数を分数関数、または有理関数という。実数係数の分数関数は、分母の多項式を一次式と二次式の累乗の積に因数分解し、その各因子を分母にもつ分数関数の和として、以下のように表すことができる。これを部分分数展開という（p(x)は多項式）。

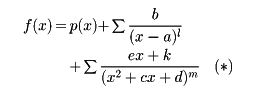
この式の意味は、f(x)が多項式p(x)と
　　b/(x-a)^l
をいくつか足し合わせたもの、および
　　(ex+k)/(x²+cx+d)^m
　　　(c²-4d＜0)
の形の項をいくつか足し合わせた形に展開されるということである。もちろん、それらの項がない場合も含めて考える。

　もっとも簡単な分数関数は、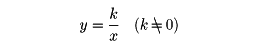

である。これは、yがxに反比例する場合で、そのグラフは、両軸を漸近線とする直角双曲線である。一般に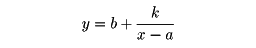

のグラフは、y=k/xのグラフをx軸方向にa、y軸方向にbだけ平行移動して得られる。

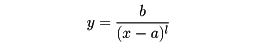
の形の分数関数は、xがaに近づくとき、yが無限大となり、y軸に平行な直線x=aは、この関数のグラフの漸近線になる。

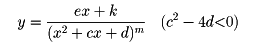
の形の分数関数では、分母のx²+cx+dはxの実数値に対しては0にならないから、関数値が無限大になるところはない。これらの分数部分は、いずれもx→±∞のとき0になる。したがって、|x|が大きい値での、グラフの形状は、（*）における多項式の部分p(x)によって決定される。p(x)が一次式mx+bならば、この関数のグラフは、直線y=mx+bを漸近線にもつ。たとえば、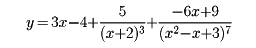

のグラフは直線y=3x-4を漸近線にもつ。

　分母・分子が一次式の分数関数、つまり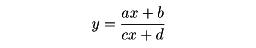

を一次分数関数という。これは、関数論における等角写像の理論、あるいは代数関数論において重要である。一次分数関数の特徴ある性質は、関数の合成に際して、係数が、ちょうど行列演算に対応して変わることである。すなわち、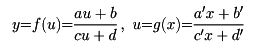

を合成したy=f(g(x))はやはり一次分数関数で、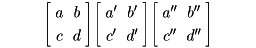

によって定められるa″、b″、c″、d″によって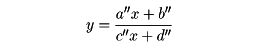

と表される。

［竹之内脩］

[参照項目] | 漸近線 | 双曲線 | 部分分数

出典　小学館　日本大百科全書(ニッポニカ)

世界大百科事典（旧版）内の分数関数の言及

【分数式】より

…分母と分子に共通因子がないとき既約分数式といい，そうでないとき可約分数式という。分数式で定義される関数を分数関数という。分母が0になる点では関数は定義されない。…

【有理関数】より

…xを変数とする有理関数f(x)は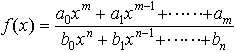，の形で表される。n＝0のときはf(x)は有理整関数，n≧1のときは分数関数という。このときf(x)の分母が0となるところでは関数は定義しない。…

※「分数関数」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」