精選版 日本国語大辞典 「双曲線」の意味・読み・例文・類語
そうきょく‐せんサウキョク‥【双曲線】
改訂新版 世界大百科事典 「双曲線」の意味・わかりやすい解説
双曲線 (そうきょくせん)
hyperbola
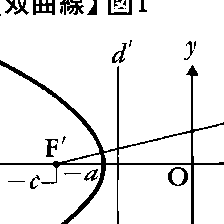
平面上で,2定点F,F′からの距離の差が正の定数であるような点によって描かれる図形を双曲線といい,FとF′をその焦点という。定数を2aとし,線分FF′の長さを2cとするとき,e=c/a(>1)を離心率という。直線FF′を横軸,線分FF′の垂直2等分線を共役軸といい,これらを合わせて主軸という。また,線分FF′の中点を中心という。横軸をx軸とし,共役軸をy軸とする直交座標系を用いるとき,上の双曲線の方程式は, となる。このときx=±a2/cで表される2直線d,d′を準線という(図1)。双曲線上の点Pから焦点F(c,0)までの距離とPから準線x=a2/cまでの距離の比は一定で離心率eに等しい。焦点F′(-c,0)と準線x=-a2/cについても同様である。|x|→∞のとき双曲線上の点は2直線y/x=±b/aに近づく。これらの直線を漸近線という(図2)。双曲線上の点Pから両方の漸近線に平行線を引くとき,それらの直線と両漸近線とで囲まれた平行四辺形の面積は一定で,ab/2となる。a=bのときは両漸近線は直交するが,このような双曲線を直角双曲線という。直角双曲線は両漸近線を座標軸にとれば,その方程式はxy=k(kは0でない定数)となる。双曲線は媒介変数θを用いて,x=a secθ,y=b tanθの形に表される(図3)。このθを双曲線上の点P(x,y)の離心角という。二つの双曲線,
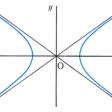
となる。このときx=±a2/cで表される2直線d,d′を準線という(図1)。双曲線上の点Pから焦点F(c,0)までの距離とPから準線x=a2/cまでの距離の比は一定で離心率eに等しい。焦点F′(-c,0)と準線x=-a2/cについても同様である。|x|→∞のとき双曲線上の点は2直線y/x=±b/aに近づく。これらの直線を漸近線という(図2)。双曲線上の点Pから両方の漸近線に平行線を引くとき,それらの直線と両漸近線とで囲まれた平行四辺形の面積は一定で,ab/2となる。a=bのときは両漸近線は直交するが,このような双曲線を直角双曲線という。直角双曲線は両漸近線を座標軸にとれば,その方程式はxy=k(kは0でない定数)となる。双曲線は媒介変数θを用いて,x=a secθ,y=b tanθの形に表される(図3)。このθを双曲線上の点P(x,y)の離心角という。二つの双曲線,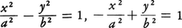 は互いに共役という(図2)。空間で直線mをこれと交わる直線lのまわりに回転したときに生ずる曲面を円錐面というが,いまlとmの交点を通らない平面πで,πのlに対する傾きがmのlに対する傾きより小さいものをとり,πで円錐面を切れば,切口は双曲線となる。この意味で双曲線は円錐曲線の一種である。この場合,πと1点で接し,円錐面と円で接する球面をとれば,πとの接点が双曲線の焦点となり,円の平面とπとの交線が準線となる(図4)。
は互いに共役という(図2)。空間で直線mをこれと交わる直線lのまわりに回転したときに生ずる曲面を円錐面というが,いまlとmの交点を通らない平面πで,πのlに対する傾きがmのlに対する傾きより小さいものをとり,πで円錐面を切れば,切口は双曲線となる。この意味で双曲線は円錐曲線の一種である。この場合,πと1点で接し,円錐面と円で接する球面をとれば,πとの接点が双曲線の焦点となり,円の平面とπとの交線が準線となる(図4)。
執筆者:中岡 稔
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「双曲線」の意味・わかりやすい解説
双曲線
そうきょくせん
hyperbola
円錐曲線(えんすいきょくせん)の一つ。平面上で二定点F、F'からの距離の差が一定な点の軌跡が双曲線であり、F、F'を焦点という()。F、F'を通る直線と、線分FF'の垂直二等分線を主軸という。主軸を座標軸とする直交座標系に関して双曲線は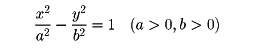
の形で表される。このとき原点Oを中心、2点(±a,0)を頂点という。また、二直線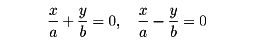
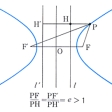
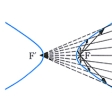
を漸近線という()。二つの漸近線が互いに直交する双曲線を直角双曲線という。のように、F'に向かって集まる光は双曲線の鏡で反射してすべてFに集まるという性質をもつ。双曲線はまた、定直線lと定点Fからの距離の比が1より大きい一定値である点の軌跡、ということもできる()。l、l'を準線、一定値eを離心率といい、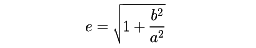
である。
[立花俊一]
ブリタニカ国際大百科事典 小項目事典 「双曲線」の意味・わかりやすい解説
双曲線
そうきょくせん
hyperbola
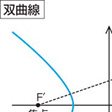
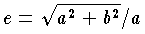 。これを双曲線の標準方程式という。線分 FF′ の中点を双曲線の中心,直線 FF′ と双曲線との交点を双曲線の頂点といい,標準形ではそれぞれ (0,0) および (a,0) ,(-a,0) となる。準線と漸近線はそれぞれ2直線 x=±a/e および x/a±y/b=0 で表わされる。また双曲線の方程式は双曲線関数を用いれば,x=a cosh t ,y=b sinh t ( t は媒介変数) で表わされる。
。これを双曲線の標準方程式という。線分 FF′ の中点を双曲線の中心,直線 FF′ と双曲線との交点を双曲線の頂点といい,標準形ではそれぞれ (0,0) および (a,0) ,(-a,0) となる。準線と漸近線はそれぞれ2直線 x=±a/e および x/a±y/b=0 で表わされる。また双曲線の方程式は双曲線関数を用いれば,x=a cosh t ,y=b sinh t ( t は媒介変数) で表わされる。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
百科事典マイペディア 「双曲線」の意味・わかりやすい解説
双曲線【そうきょくせん】
→関連項目反比例
出典 株式会社平凡社百科事典マイペディアについて 情報
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...


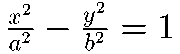 という形の
という形の