分数式（読み）ブンスウシキ

デジタル大辞泉

ぶんすう‐しき【分数式】

整式を整式で割る形をしている式。

出典　小学館

精選版 日本国語大辞典

ぶんすう‐しき【分数式】

1. 〘 名詞 〙 二つの整式Ａ、Ｂの商を横線を用いてA/Bと表わしたもの。Ｂが一次以上の整式であるものをさすことが多い。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

分数式
ぶんすうしき

A、Bをそれぞれいくつかの文字（とくに変数）についての有理整式（多項式）とし、Bは恒等的にゼロでない（係数のうち少なくとも一つはゼロでない）とする。式A/Bをこれら文字についての分数式（または有理式）という。Aを分子、Bを分母といい、分子の次数が分母の次数より小さいとき真分数式、そうでないとき仮分数式という。また、分母と分子が定数以外に公約数をもたないとき、既約(きやく)、そうでないとき可約であるという。可約な場合、分母分子の公約数を消し去ることを約分する（約す）という。たとえば、
　　(x²+2x-3)/(x²-1)
を約分して
　　(x+3)/(x+1)
が得られる。

　分数式の相等・四則は次のように定義される。

　分母分子がまた分数式であるものを繁分数式(はんぶんすうしき)という。繁分数式は四則計算により通常の分数式に帰着される。与えられた分数式を複数の分数式の和で表すことを部分分数分解という。一般に既約真分数式の分母が、互いに公約数をもたない因数に分解されるとき、与えられた分数式はこれら因数をそれぞれ分母とする既約真分数式の和として、一通りに表される。たとえば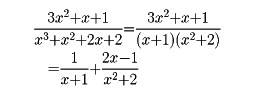

部分分数分解には一般に未定係数法が用いられる。また部分分数分解は分数式の積分法に用いられる。

［竹内芳男］

[参照項目] | 未定係数法

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

分数式 (ぶんすうしき)
fractional expression

f（x），g（x）を二つの多項式とするとき，

の形の式をxに関する分数式という。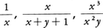

などはその例である。分母と分子に共通因子がないとき既約分数式といい，そうでないとき可約分数式という。分数式で定義される関数を分数関数という。分母が0になる点では関数は定義されない。

（kは定数）
　のグラフは，図の形の双曲線である。

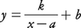のグラフは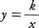，のグラフをx軸方向にa，y軸方向にbだけ平行移動したものである。
執筆者：上野 健爾

図－分数式

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

分数式
ぶんすうしき

「有理式」のページをご覧ください。

出典　ブリタニカ国際大百科事典 小項目事典