双曲型方程式（読み）そうきょくがたほうていしき（その他表記）hyperbolic equation

改訂新版　世界大百科事典

双曲型方程式 (そうきょくがたほうていしき)
hyperbolic equation

偏微分方程式の一つ。双曲型方程式の基本的な形は，

　∂²u/∂t²＝c²⊿u　　　……（1）　

　　（⊿＝∂²/∂x₁²＋……＋∂²/∂x_n²）　

と書かれる。ここでcは正の定数である。物理的には振動や波動を記述する方程式であって，未知関数u＝u（t，x）は点x＝（x₁，……，x_n）の時刻tにおける変位を表す。通常，方程式（1）の解で初期条件，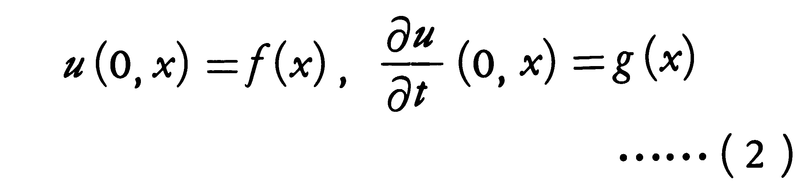

を満たすものを求めることが問題になる。これを双曲型偏微分方程式の初期値問題という。

　空間次元nが1（例えば弦の振動，または直線上を進む波）の場合は，方程式（1）は，

　∂²u/∂t²＝c²∂²u/∂x²　　……（1′）　

と書ける。φ（x），ψ（x）を2回微分可能な任意の関数とするとき，

　u（t，x）＝φ（x＋ct）＋ψ（x－ct）　　　……（3）　

は（1′）の解である。（3）の右辺の第1項はx軸上を速度cで左方に進む波を表し，第2項は速度cで右方に進む波を表している。（1′）の解で初期条件（2）を満たすものは，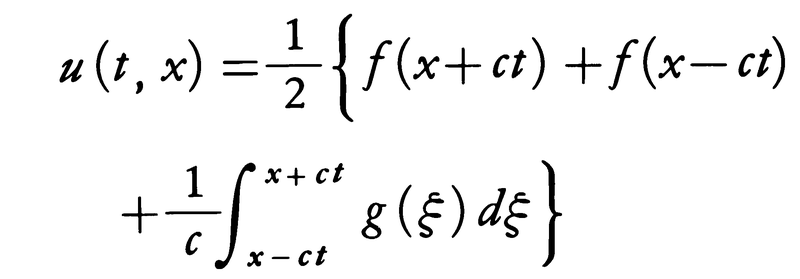

で与えられる。ただしfは2回微分可能な関数，gは1回微分可能な関数とする。これをストークスの波動公式という。

　三次元空間（n＝3）の場合の（1）の解で初期条件（2）を満たすものは次の式（4）で表される。まず点x＝（x₁，x₂，x₃）を中心とする半径rの球面S_x，_r上での関数fの平均値をM_x，_r［f］と書く。すなわち，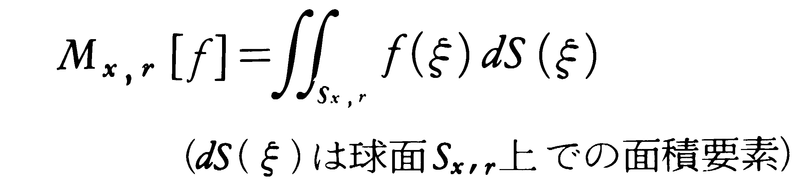

このとき，初期値問題（1）-（2）の解u（t，x）は，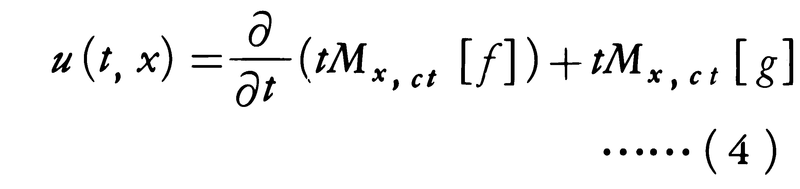

と書ける。これをポアソンの波動公式という。
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

世界大百科事典（旧版）内の双曲型方程式の言及

【偏微分方程式】より

…
［振動･波動の問題］
　振動，または波動の現象では，時刻tにおける点xの変位u(t,x)があまり大きくないときは，それが時間tとともに変化する状態は次の方程式で記述される。この形の方程式を双曲型方程式，または波動方程式という。　(4)においてfが変数tを含まない場合で，温度が平衡状態にあるとき，すなわちuが時間とともに変化しないときは，∂u/∂t＝0であるから，(1/c)f(x)をあらためてf(x)と書けば，(4)は，　Δu＝－fとなる。…

※「双曲型方程式」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」