デジタル大辞泉
「中心」の意味・読み・例文・類語
出典 小学館デジタル大辞泉について 情報 | 凡例
Sponserd by 
ちゅう‐しん【中心】
- 〘 名詞 〙
- ① まんなか。中央。
- [初出の実例]「門の中心にあたる所に木をうふることははばかるべし」(出典:作庭記(1040頃か))
- [その他の文献]〔白居易‐雲居寺孤桐詩〕
- ② こころのそこ。むねのうち。心中(しんちゅう)。胸中。内心。
- [初出の実例]「被仰之事甚多、中心難忍者也」(出典:権記‐長保二年(1000)一二月二〇日)
- 「伝奏諸の憤を恐て、終に奏聞せざりければ、上天听を隔て中心の訴へ啓けず」(出典:太平記(14C後)一二)
- [その他の文献]〔詩経‐小雅・隰桑〕
- ③ 主だったものが集中する場所。また、非常に重要な所、もの、人。枢要。
- [初出の実例]「雖レ為二無勢一、中心之所レ之在二武衛一」(出典:吾妻鏡‐治承五年(1181)閏二月二三日)
- ④ =ちゅうしん(衷心)
- [初出の実例]「賤妾中心歓未レ尽、良人上馬遠従レ征」(出典:文華秀麗集(818)中・奉和春閨怨〈朝野鹿取〉)
- [その他の文献]〔論語‐学而〕
- ⑤ 数学用語。
- (イ) 円周上、または、球面上のすべての点から等距離にある点。
- [初出の実例]「日は緯星行輪中心に在りて、而して小界の中心に在らず」(出典:窮理通(1836)一)
- (ロ) 楕円、双曲線、楕円体などをある点に関して対称な図形と見たときのその点。
- (ハ) 群のすべての要素と交換可能な要素の全体の作る群。
- ⑥ 重心のこと。
- [初出の実例]「稍ともすると中心を失って倒れかかる」(出典:吾輩は猫である(1905‐06)〈夏目漱石〉二)
出典 精選版 日本国語大辞典精選版 日本国語大辞典について 情報 | 凡例
Sponserd by 
中心
ちゅうしん
center
(1) 幾何学に関して 円,球,楕円,双曲線などの中心,反転の中心などがある。 (2) 群に関して 群 G において,すべての元 x ∈ G に対し,xc=cx であるような元 c の全体 C を G の中心という。すなわち,G のあらゆる元と交換可能な元全体から成る集合をいう。中心 C は,G の正規部分群となる。 (3) 環に関して 環 R の部分集合 S において,すべての元 x ∈ S に対し,xc=cx を満たすような元 c ∈ R の全体 C(S) を,環 R の中心という。中心 C(S) は R の部分環になる。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
普及版 字通
「中心」の読み・字形・画数・意味
【中心】ちゆうしん
まん中。また、心中。〔詩、王風、黍離〕行き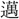 (ゆ)くこと靡靡(びび)たり 中心
(ゆ)くこと靡靡(びび)たり 中心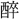 へるが如し
へるが如し字通「中」の項目を見る。
出典 平凡社「普及版 字通」普及版 字通について 情報
Sponserd by 
世界大百科事典(旧版)内の中心の言及
【群】より
…n≧2のとき,二つの場合(n=2で,Kの元数2または3)を除いて,G/Nは単純群である。
[中心]
群Gにおいて,Z={x∈G|どんなy∈Gに対してもxy=yx}は正規部分群である。これをGの中心という。…
※「中心」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by 
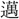 (ゆ)くこと靡靡(びび)たり 中心
(ゆ)くこと靡靡(びび)たり 中心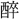 へるが如し
へるが如し