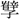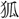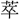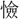目次 群の歴史 ガロア群 の例 部分群 可解群 指数と位数 単純群 中心 群の表現 二面体群,正多面体群 正の数全体の集合P を考えてみると,これらは次の4条件を満たしている。(1)a ,b がP の元であれば,その積a ×b が定まって,a ×b もP の元である。(2)結合法則,すなわち(a ×b )×c =a ×(b ×c )が成り立つ。(3)1×a =a ×1=a (単位元1が存在する)。(4)a ×a ⁻1 =a ⁻1 ×a =1(逆元a ⁻1 が存在する)。
一般に,数の乗法に限らず,ある集合G に一つの演算(数の加法,写像の合成など)が定義されていて,それが上のような4条件を満たしているとき,G は群であるという。演算の記号は,具体例では,×,+,◦などいろいろありうるので,一般的に*で表すことにすると,定義は次のように述べられる。
集合G に一つの演算*が定義されていて,すなわち,(1)a ,b がG の元ならば,a *b が定まって,G の元であり,さらに次の3条件(2)~(4)が満たされているとき,G はこの演算*に関して群をなすという。(2)結合法則,すなわち(a *b )*c =a *(b *c )が成り立つ。(3)適当な元e があって,G のどの元a に対しても,e *a =a *e =a となる。このe をG の単位元という。(4)G の各元a に対して,a *b =b *a =e となるような元b が存在する。このb をa の逆元という。
演算を加法と呼ぶときは演算の記号としては+を用いるのがふつうで,この場合単位元を0で表し,零と呼び,またa の逆元を-a で表し,マイナスa と呼ぶ。
演算を乗法と呼ぶときは,演算の記号は略す(a *b をab とかく)か,・を用いるのがふつうであり,単位元を1で表すことが多い。a の逆元はa ⁻1 で表す。
数の加法や乗法の場合には,条件(5)交換法則,すなわちa *b =b *a が満たされている。このような場合,可換群 またはアーベル群 と呼ぶ。今後,この項では群の演算の記号は省略して,積はab のようにかく。
数の加法や乗法とは異なる演算で群をなす例として対称群 (置換群 )があるが,それ以外の簡単な例を一つあげよう。
テーブルの上に裏,表の区別のできる板をおいた場合を考える。板を裏返す操作をa とし,何もしないのをe としよう。a を2回繰り返したaa を考えると,もとの状態に返るから,aa =e 。そして,a とe の二つの元だけで群になる。今は板の裏表だけを考えて置くときの板の向きは考えなかったが,向きも考えに入れて同様の操作を考えると,だいぶ複雑な群ができる。
群の歴史 五次以上の方程式 の解法を見いだす努力として,J.L.ラグランジュ とバンデルモンドAlexis Théophile Vandermonde(1735-96)が,1770年ころに三次,四次の場合の解法を吟味して,根の整式に根の置換をほどこしたとき,どれだけ異なった値をもつかということなどに着目した。約半世紀後にN.H.アーベル とE.ガロア がその考えを進展させて,アーベルが,まず代数的に解ける多項式 (係数から出発して,根が四則算法とべき根 をとる演算とで得られるもの)を調べ,一般の五次多項式には代数的には解けないものがあることを示した。ガロアはさらに進んで,多項式の群(今日の言葉でいうガロア群)を考え,また,根をつけた体やその中間体も定義して,ガロア群の構造と中間体との関係を解明した。また,後に述べる正規部分群を定義したのもガロアであり,このガロアの研究が群論の始まりといえる。ガロアの理論は,1870年に出版されたC.ジョルダンの著書に詳しく紹介されている。扱った群は一つの方程式の根の置換群であり,その後,A.L.コーシーはもっと一般な置換群を扱ったが,初めに述べたような抽象的な定義は,ケーリーArthur Cayley(有限群 の場合)およびL.クロネッカー(一般の場合)による。このように抽象的な群の概念に到達してみると,群と幾何学 との関係が浮かび上がり,F.クラインの有名な《エルランゲン・プログラム》がそれを明確にした。その後,群の概念は,代数学 ,幾何学だけでなく,数学の多くの分野において,たいへん基本的なものになった。また,結晶学における結晶の分類や,量子力学 にも応用されている。群に位相を入れた位相群 というものもあり,その応用範囲は広い。応用される分野に応じて群があるといえるくらい,重要な群が多くあり,その多くのものはリー群 と呼ばれるものに含まれる。
ガロア群の例 方程式x 6 -2=0のガロア群を求めてみよう。1の虚立方根の一つをωとすれば,-ωが1の6乗根であり,上の方程式の6根は±6 \(\sqrt{2}\),±ω 6 \(\sqrt{2}\),±ω2 6 \(\sqrt{2}\)である。ガロア群G の元φは6根を独立に考えての置換ではなく,数の体系としてふさわしいものと考えることにすれば,6 \(\sqrt{2}\)とωの写され先(前者は6根のどれか,後者はωかω2 )がきまれば,他の根の写る先もきまる
σ,σ2 ,σ3 ,σ4 ,σ5 ,σ6 =1
τσ,τσ2 ,τσ3 ,τσ4 ,τσ5 ,τ
の12個の元は互いに異なるG の元になる。6 \(\sqrt{2}\)の行先は六つ,ωの行先は二つゆえ,G の元は,6×2=12より多くはあり得ないから,上の12個の元がガロア群を作るのである。この群では,σ6 =1のほかに,τ2 =1,τστ=σ5 =σ⁻1 (τστはω→ω,6 \(\sqrt{2}\)→-ω2 6 \(\sqrt{2}\)と写すから)という関係がある。
可解群という概念(後述)があるが,方程式が代数的に解けるためには,そのガロア群が可解群であることが必要十分条件である。
定規とコンパス だけでは3等分のできない角θの存在することが知られているが,その証明には,
部分群 例えば,正の数全体が乗法に関して作る群P の中で,3m 5n (m ,n は整数)の形の数全体H をとれば,H ⊂P であって,H だけでも群になっている。このように,一つの群G の部分集合K が,それ自身でも群になっているとき,K はG の部分群であるという。この例H は,3と5を含む最小の部分群であるという意味で,3と5とで生成された部分群であるといい,〈3,5〉で表すことが多い。一つの元a で生成される群〈a 〉={a n |n =0,±1,±2,……}を,a で生成された巡回群 という。一般に,群G の部分群K が与えられたとき,a ,b ∈G により,Ka ={ka |k ∈K }とKb ={kb |k ∈K }とに共通元があれば,Ka =Kb である。そこでKa の形の集合全体を考えると,G を共通元をもたない部分集合の和に分けることになる。Ka を,K を法とする右剰余類 (“右”は,K の元によりずらした余りに相当するa が右側にあるから)または左K 剰余類(“左”はK が左側にあるから)という。左,右を逆にしたaK の形の部分集合も考えられるが,この左右の区別のいらない場合,すなわち,〈k ∈K ,a ∈G ならば,a ⁻1 ka ∈K 〉の成り立つとき,K はG の正規部分群であるといい,各Ka を,K を法とする剰余類という。剰余類全体は,(Ka )(Kb )=Kab と乗法を定義すると新しい群ができる。この群を剰余類群 と呼び,G /K で表す。この事情は整数全体Z が加法に関して群であり,一つの整数n の倍数全体nZ が部分群になり,n で割って余りが同じになるものをひとまとめにしたものが各剰余類であることを思い浮かべれば理解の助けになろう。
可解群 H ,K が群G の部分群であるとき,{h ⁻1 k ⁻1 hk |h ∈H ,k ∈K }を含む最小の部分群を,H とK との交換子群といい,[H ,K ]で表す。[H ,H ]をD (H )と表すことにする。G =G 0 とおき,Gi + 1 =D (Gi )と定めたとき,G =G 0 ⊇G 1 ⊇……⊇Gn ⊇……となるが,あるn でGn が単位元だけになるとき,G は可解群であるという。次のような部分群の列があるといっても同じである。G =H 0 ⊃H 1 ⊃……⊃Hm ={単位元},各Hi (i =1,2,……,n )はHi - 1 の正規部分群で,Hi - 1 /Hi がアーベル群。
方程式が代数的に解けるための条件は,ガロア群がこの性質をもつことであるという理由で,このように名づけられたのである。
指数と位数 H が群G の部分群であるとき,互いに異なる右剰余類Ha の数(無限の場合も考える)をH のG における指数という。[G :H ],(G /H )などで表される。これは左剰余類で定義しても同じになる。G の元の数をG の位数といい|G |,♯(G )などで表される。これが有限である場合には,有限群と呼ぶ。G の元a について,a で生成された巡回群〈a 〉の位数をa の位数という。|G |が有限である場合,各Ha はH と同じ個数の元からなるから,|G |=[G :H ]×|H |が得られ,部分群Ha の位数,指数はG の位数の約数であることがわかる。
単純群 群G の正規部分群が,G と{単位元}以外にはないとき,G は単純群であるという。n ≧5のとき,n 次交代群(置換群 )は単純群である。このことは五次以上の方程式が一般には代数的に解けないことと関連する。体K の上のn 次特殊線形群 G の中で,スカラー行列全体N は,正規部分群であるので,G /N を考えることができる。n ≧2のとき,二つの場合(n =2で,K の元数2または3)を除いて,G /N は単純群である。
中心 群G において,Z ={x ∈G |どんなy ∈G に対してもxy =yx }は正規部分群である。これをG の中心という。上の特殊線形群G の場合,N が中心になっている。
有限群G の位数が素数p のべきpe であるとき,G はp 群であるという。e ≧1であれば,G の中心の位数はpm (m ≧1)である。したがって,次のような部分群の列がある。{単位元}=Z 0 ⊂Z 1 ⊂……⊂Zs =G ,各i =1,2,……,s について,Zi /Zi - 1 はG /Zi - 1 の中心。したがって,p 群は可解群である。
群の表現 一つの群G を調べるのに,他の群H への準同型 φを考え,φの核φ⁻1 (1)={x ∈G |φ(x )=1(単位元)}およびφ(G )を調べることが有効であることがある。このようなφ,H を考えることをG の表現という。H が線形群であるのが通例であり,群の表現論といえば,そのような表現に関する理論を意味するのがふつうである。その他の型の表現の例として,置換表現がある。H が群G の部分群で,g ∈G に対しn 個の集合a 1 H ,……,an H の上の置換,
a 1 H a 2 H ……an H
ga 1 H ga 2 H ……gan H
を対応させると,G からn 次の対称群の中への準同型が得られるのである。
二面体群,正多面体群 正n 角形F の位置を定めた上で,F の回転および裏返しによるF からF への変換は,回転がn 個,裏返しと回転の合成がn 個,合計2n 個の元からなる群を作る。このような群を二面体群という。正多面体 には,正四面体,正六面体 (すなわち立方体 ),正八面体 ,正十二面体,正二十面体がある。正n 面体K の位置をきめ,K の中心を中心とする回転で,K の位置を変えないもの全体の作る群をn 面体群といい,それらを総称して,正多面体群 という。四面体群は四次交代群と同型で,位数は12である。六面体群,八面体群,四次対称群は同型で,位数は24である。十二面体群,二十面体群,五次交代群は同型で,位数は60である。永田 雅宜
 〈グン〉
〈グン〉 〈むら〉「
〈むら〉「

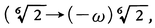
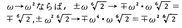 のように)。そこでσ,τを,
のように)。そこでσ,τを,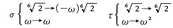 によって定めると,
によって定めると,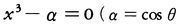
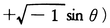 のガロア群が利用できる。その場合,作図可能なのは,ガロア群の元が2個以内のときであり,例えば,θ=60°でも,ガロア群の元数は六つである。このように,ガロア群は方程式の解法以外にも応用がある。
のガロア群が利用できる。その場合,作図可能なのは,ガロア群の元が2個以内のときであり,例えば,θ=60°でも,ガロア群の元数は六つである。このように,ガロア群は方程式の解法以外にも応用がある。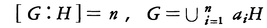 であるとき,各g∈Gに対しn個の集合a1H,……,anHの上の置換,
であるとき,各g∈Gに対しn個の集合a1H,……,anHの上の置換,

 〕に「
〕に「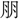 なり」と訓するが、もと獣の群集する意である。〔詩、小雅、無羊〕は牧場開きを祝う詩で、「三百維(こ)れ群す」とその多産を予祝する。羊や鹿の類には群集する習性があるので、羊には群といい、鹿には
なり」と訓するが、もと獣の群集する意である。〔詩、小雅、無羊〕は牧場開きを祝う詩で、「三百維(こ)れ群す」とその多産を予祝する。羊や鹿の類には群集する習性があるので、羊には群といい、鹿には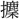 (くん)という。これを人に移して群衆という。金文の〔陳侯午敦(ちんこうごたい)〕に「群
(くん)という。これを人に移して群衆という。金文の〔陳侯午敦(ちんこうごたい)〕に「群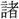 侯」の語がみえている。
侯」の語がみえている。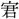 ・
・ giu
giu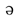 nは同声。
nは同声。 khyu
khyu