日本大百科全書(ニッポニカ) 「変格積分」の意味・わかりやすい解説
変格積分
へんかくせきぶん
有界でない関数や、有限でない区間にまで積分の意味を拡張して考えたものをいう。広義積分、仮性積分、特異積分、異常積分などともいう。通常の定積分は、区間［a,b］で連続、したがって有界な（とりうる値の範囲が上下に限られた）関数について定義されている。たとえばf(x)=1/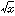
は、半開区間（0,1］（0＜x≦1を満たすx全体のつくる区間）上では連続であるが、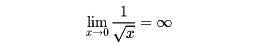
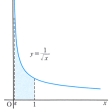
であるから有界ではない（）。したがってこの関数に対して定積分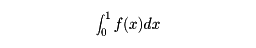
を考えることは、定積分の設定をはみだしている。ところが0＜ε＜1なる任意のεに対して、閉区間［ε,1］上ではf(x)=1/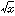は定積分可能で、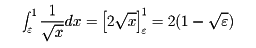
となる。そこで、この積分値の極限値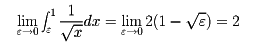
をもって、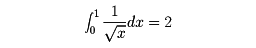
とするのは自然である。一般に、関数f(x)が（a,b］（a＜x≦bを満たすx全体のつくる区間）で定義され、そこで連続であるとする。このときa＜α＜bなるαを任意にとれば、f(x)は［α,b］で連続、したがって、積分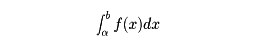
が定まる。もしこのとき、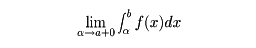
が存在するならば、この値を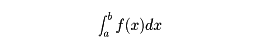
と書き、これをf(x)の変格積分という。f(x)が［a,b）で連続の場合、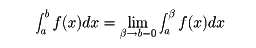
f(x)が(a,b)、すなわち、a＜x＜bを満たすx全体のつくる区間で連続の場合、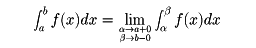
とする（α、βに関する極限は独立にとる）。これらの極限値が存在して有限な値となるとき、積分は収束するという。また、もしこれらの極限が存在しないときは、積分は存在しないという。たとえば、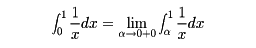
については、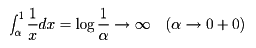
であるから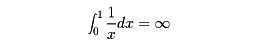
である。また冒頭の例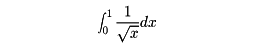
については、積分は収束して、その値は2、ということになる。積分区間内にいくつかの関数値の定義されない点を含む場合には、それらの点で区間を分割したうえで変格積分を考える。たとえば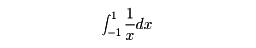
については、0のところで分けて、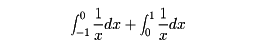
と考える。そうするとこれは(-∞)+∞となるが、このようなときは積分は存在しないとする。同様に無限区間における変格積分を考える。
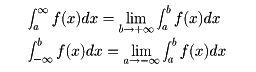
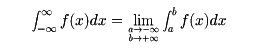
によって、右辺の極限が存在するとき、その値を左辺の定積分の値と定める。たとえば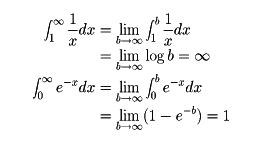
である。
［竹之内脩］
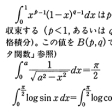
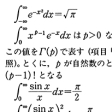
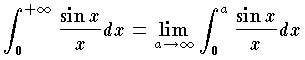のように，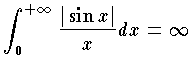
であるにもかかわらず，収束する積分のことをいう。