対称式（読み）タイショウシキ

デジタル大辞泉

たいしょう‐しき【対称式】

式の中のどの二つの文字を交換しても値の変わらない式。例えば、x²＋y²＋z²など。

出典　小学館

精選版 日本国語大辞典

たいしょう‐しき【対称式】

1. 〘 名詞 〙 整式または有理式の一つ。そのどの二つの文字を交換しても変わらないようなものをいう。たとえば x²+y²+z², xy+yz+zx などはｘ、ｙ、ｚの対称式である。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

対称式
たいしょうしき

2個以上のn個の変数X₁、……、X_nの多項式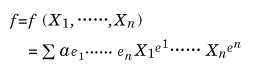

が、任意の1≦i＜j≦nなるiとjに対し、fに現れるX_iとX_jを互いに他と置き換えても、多項式として変わらないとき、つまり
　　f(X₁,……,X_i,……
　　　,X_j,……,X_n)
　　　=f(X₁,……,X_j,……
　　　,X_i,……,X_n)
のとき、fを対称式という。

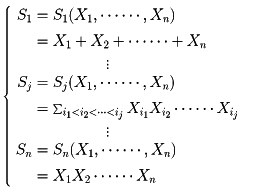
は、対称式である。さらに、任意のn変数の対称式は、これらn個の対称式S₁、……、S_nの多項式で表される。この意味で、S₁、……、S_nをn変数の基本対称式という。たとえば、三変数の基本対称式は、
　　S₁=X₁+X₂+X₃,
　　S₂=X₁X₂+X₁X₃+X₂X₃,
　　S₃=X₁X₂X₃
で、X₁²+X₂²+X₃²=S₁²-2S₂
となる。

　n変数の対称式fは、1、2、……、nの任意の置換σに対し、
　　f(X_σ(1),X_σ(2),……,X_σ(n))
　　　=f(X₁,X₂,……,X_n)
を満たす。また、多項式fが対称式であることを示すには、i=1,2,……,n-1に対し、X_iとX_i+1を互いに他と置き換えて、変わらないことを確かめればよい。

　多項式f(X)=Xⁿ+a₁X^n-1+……+a_n-1X+a_nの根をα₁、……、α_nとすると、いわゆる根と係数との関係式
　　a_j=(-1)^jS_j(α₁,……,α_n)
　　　(j=1,……,n)
が成り立つ。このように、対称式は広く応用されている。

［菅野恒雄］

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

対称式 (たいしょうしき)
symmetric expression

n変数の多項式，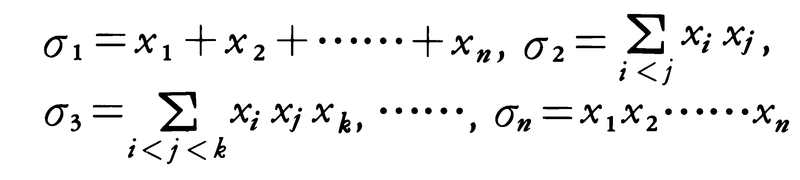

において，変数x₁，x₂，……，x_nをどのように置換しても各多項式は変わらない。このような多項式を対称式という。対称式には上記以外にもx₁²＋x₂²＋……＋x_n²などたくさんあるが，すべての対称式はσ₁，σ₂，……，σ_nの多項式で書ける。例えば，x₁²＋x₂²＋……＋x_n²＝σ₁²－2σ₂である。これからわかるようにσ₁，σ₂，……，σ_nは基本的なものであり，基本対称式と呼ばれる。一般に体k上の多項式環k［x₁，……，x_n］に群Gが作用している（α∈G，f（x₁，……，x_n）∈k［x₁，……，x_n］に対して，多項式（αf）（x₁，……，x_n）が定まり，f→αfは環準同型，（αβ）f＝α（βf），単位元eについてはef＝f，≏α∈G，≏a∈k，αa＝a）のとき，≏α∈Gについてαf＝fとなる元をGの作用についての不変式といい，その全体をk［x₁，……，x_n］^gと書く。k［x₁，……，x_n］^gはk［x₁，……，x_n］の部分環である。対称式はn次対称群S_nがk［x₁，……，x_n］に変数の置換として作用するときの不変式であり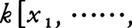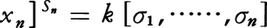，となることが上に述べたことである。
執筆者：丸山 正樹

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

対称式
たいしょうしき
symmetric form

変数 X₁ ，X₂ ，…，X_n の多項式 f(X₁ ，X₂ ，…，X_n) が X₁ ，X₂ ，…，X_n の置換で変らないとき，対称式という。3変数 a ，b ，c でいえば，a＋b＋c ，bc＋ca＋ab ，abc などは対称式である。この種の形のものを基本対称式といって，一般の対称式は基本対称式を用いて表わせる。

出典　ブリタニカ国際大百科事典 小項目事典