微分法（読み）びぶんほう（その他表記）differential calculus

日本大百科全書(ニッポニカ)

微分法
びぶんほう
differential calculus

関数の導関数を求めたり、それらを利用して関数の性質を調べたりする数学の分野。17世紀後半、ニュートン、ライプニッツによって始められた。たとえば、ある瞬間の車の速さは、平均速度（ある時間に車の動いた距離を時間で割った値）の、時間を0に近づけた極限の値である。同じことを一般の関数について考えてみる。

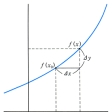
　関数y=f(x)において、xがx₀の近くにあるとき、x-x₀をΔxで表し、xの増分という。またf(x)-f(x₀)をΔyで表し、yの増分という。

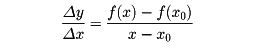
は、xの変化Δxに伴うyの平均変化率である。Δxを限りなく0に近づけたとき、この平均変化率がある極限値に近づくならば、f(x)はx=x₀で微分可能であるといい、その極限値を微分係数といって、f′(x₀)で表す。関数は、微分可能ならば、その点で連続である。

　なお、微分積分法の諸定理を導く基礎となる重要な定理に、「平均値の定理」があるが、これについては、その項目を参照されたい。

［竹之内脩］

導関数

関数f(x)に対して、各点においてその点での微分係数の値を対応させる関数をf(x)の導関数といい、f′(x)で表す。そして、導関数f′(x)を求めることを、f(x)を微分するという。ニュートンは、導関数を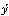で表し、流率とよんだ。この記号は、現在、とくに時刻に関して微分した導関数を表すときによく用いられる。ライプニッツは、Δy/Δxの極限の意味でdy/dxと書いて、これを微分商とよんでいる。基本的な関数の導関数は表1に示したとおりである。また、関数を微分するための諸公式を表2に示した。微分の計算は、これらを組み合わせて実行される。

［竹之内脩］

高階導関数

一般論でいうと、関数が至る所微分可能でも、導関数が連続であるとは限らない。しかし、われわれが用いる関数は、都合よく、何回でも微分できるのが普通である。関数y=f(x)の導関数f′(x)がさらに微分可能であるとき、その導関数をf″(x)、さらに微分可能であればその導関数をf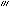(x),……として、次々に導関数が得られる。k回微分して得られる導関数をk階導関数（またはk次導関数）といい、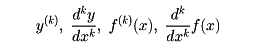

などと書く。積のk回微分をするのには、ライプニッツの公式が著名である（表2）。

　関数f(x)のk階の導関数（したがって当然、すべての1≦j≦kであるjについてのj階導関数）が存在して連続であるとき、f(x)はC^k級関数という。また、すべてのk=1,2,……についてk階の導関数が存在するとき、C^∞級関数という。

　関数f(x)がx=aの近傍で無限回微分可能であるとき、次の級数を、x=aの周りのf(x)のテーラー級数という。

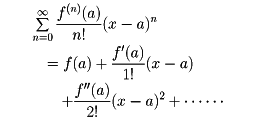
［竹之内脩］

微分法と関数値の増加・減少

微分法の一つの重要な効用は、それによって、関数の増加・減少の状態を知ることができる点にある。すなわち、ある区間で、つねにf′(x)≧0であれば、関数はこの区間で単調に増加するし、f′(x)≦0であれば単調に減少する。

　f(x)がx=x₀のある近傍で、x₀において最大になっているとき、x₀で極大という。極小についても同様に定義される。f(x)が微分可能な関数であれば、極大あるいは極小になる点では、f′(x₀)=0である。この逆は一般に成立しない。数学では、関数が最大あるいは最小となる点を求めることが要求されることが多い。f′(x)=0は極大・極小のための必要条件にすぎないが、これらの点を調べていくことにより、有効に、最大・最小を与える点を探すことができる。微分法は、このための重要な手段を提供している。

　多変数関数の微分法については、「偏微分法」の項目を参照されたい。

［竹之内脩］

[参照項目] | 最大・最小 | テーラー級数 | 微分積分法 | 平均値の定理 | 偏微分法

微分法説明図

基本的な関数の導関数〔表1〕

微分法の公式〔表2〕

出典　小学館　日本大百科全書(ニッポニカ)

世界大百科事典（旧版）内の微分法の言及

【微分】より

…この瞬間的な変化の考えを数学的に厳密に定式化すると，すぐ後に説明するところの微分係数，導関数の概念に到達する。与えられた関数の微分係数や導関数を求める演算を微分法differential calculusという。微分法のことを単に微分ということが多いが，これは〈微分することdifferentiation〉からきた略称である。…

※「微分法」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」