振子の振動（読み）ふりこのしんどう

最新 地学事典

ふりこのしんどう
振子の振動

vibration of pendulum

lという長さの糸でつられた質点振子の支点にa₀sinωtのような簡単な単振動が加わった場合，この振子の質点についての運動方程式は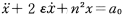，ω²sinωtとなる。ここで，左辺の第2項は速度に比例した抵抗力を，第3項は変位に比例した復元力を示す。この項のnは（は重力加速度）に等しく，この振子の固有周期をTとすればn＝2π/Tに相当する。この運動の式を解くと，

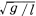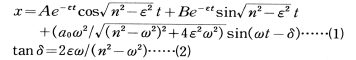
となる。（1）式の初めの2項は，この振子の自由振動を示す項で，固有の周期2π/nよりもやや大きな2π/ 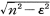という周期で揺れながら，その振幅は時間tとともにe^－εtで減衰していく。無次元量h＝ε/nを減衰定数（damping coefficient）という。第3項は，外部からの振動a₀sinωtによって強制的に振らされているための強制振動（forced oscillation）を示す項で，外部からの振動に対していつも（2）で示されただけの位相の遅れ（δ）をもつが，同じ周期2π/ωで揺れる。しかしその振幅は，もとの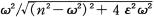倍になっている。この倍率を周期係数と呼ぶ。この式は，n/ω＝uと書き直し，前述のhを使うと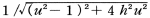となる。

執筆者：三東 哲夫

しんしのしんどう
振子の振動

oscillation of pendulum

⇒ 振子ふりこの振動

出典　平凡社「最新 地学事典」