振子（読み）フリコ（英語表記）pendulum

デジタル大辞泉

ふり‐こ【振（り）子】

定点を中心にして一定周期で振動する物体。単振り子・実体振り子・円錐振り子などがある。

しん‐し【振子】

「振り子」に同じ。

出典　小学館

精選版 日本国語大辞典

しん‐し【振子】

1. 〘 名詞 〙
2. ① ＝ふりこ（振子）
   1. [初出の実例]「窓より洩るる梭の音の、絶間なき振子の如く」(出典：薤露行（1905）〈夏目漱石〉二)
3. ② 節分で、鬼やらいをする者につき従う子供たち。→侲子。〔東京年中行事（1911）〕

ぶりっ‐こ【振子】

1. 〘 名詞 〙 いかにもかわいくていい子のようにふるまう人。特に、若い女性にいう。昭和五五年（一九八〇）頃から流行した語。
   1. [初出の実例]「私がハマトラを何としても気にくわないのは、それが『かわい子ぶりっこルック』『どうってことないルック』だからで」(出典：にんげん動物園（1981）〈中島梓〉七一)

ふり‐こ【振子】

1. 〘 名詞 〙 一定点あるいは一定軸の周囲を一定の周期で振動する物体。単振り子、実体振り子、円錐振り子などがある。しんし。〔物理学術語和英仏独対訳字書（1888）〕
   1. [初出の実例]「柱時計の振子(フリコ)の様に」(出典：坑夫（1908）〈夏目漱石〉)

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

振子 (ふりこ)
pendulum

〈しんし〉ともいう。ひもまたは棒の一端を支えて他端におもりをつるしたもので，固定点または固定軸のまわりで周期運動（ふつうは鉛直面内で円周に沿った振動）をする物体をいう。もっとも単純化した振子は質量がなく伸縮しないとした糸で質点をつるしたもので，これを質点振子といい，質点振子を重力の作用下で，一つの鉛直面内で振動させるものを単振子と呼ぶ。支点での摩擦も質点に対する空気抵抗も作用しないとしたとき，質点に働く力は図に示すように，重力と糸の張力で，その合力はつねに質点を円周の最下点Qに引き戻す向きに働くから，質点はQを中心として振動する。その周期Tは，振幅が大きくない場合には糸の長さをl，重力加速度をgとすると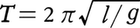，である。すなわち，周期はおもりの質量には関係しない。振幅が大きくなると周期は最大の振れの角αによって変化し，その値は近似的に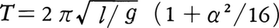，となる。振幅が小さい範囲で振子の周期が振幅とは無関係に一定である性質を振子の等時性という。

　実際の振子は多くの場合，変形しないじょうぶな棒の一端におもりを取り付け，なめらかな軸受け，またはナイフエッジで支えて水平な軸のまわりに回転できるようにしたものである。このような振子を実体振子，または物理振子という。その周期Tは，振子の回転軸のまわりの慣性モーメントをI，振子の質量をM，回転軸から重心までの距離をhとすると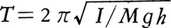，で与えられる。振子の重心のまわりの慣性モーメントI_GをMk²とおくと，I＝M（k²＋h²）の関係があるので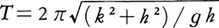，と書き換えることができる。これは長さが（k²＋h²）/hの単振子の周期に等しい。この単振子を相等単振子という。上の周期の式は，あるTとkとの値に対してhを定める二次方程式と考えることができる。その場合，対応するhの値は一般に二つあり，それらをh₁，h₂とすると，

　h₁＋h₂＝gT²/4π²

の関係がある。そこで一つの振子の重心をはさんで反対側にそれぞれ支点P₁，P₂を選び，どちらを支えて振らせても周期が等しいようにすると，上の関係から重心の位置がわからなくても，P₁とP₂の距離がわかっていればTを測定してgを求めることができる。この性質を利用して重力加速度gを求めるためにくふうされたのがケーターの可逆振子（ケーター振子ともいう）で，両端に支点のナイフエッジを設け，おもりの位置を動かして周期を調節できるようにしてある。

種々の振子

質点がサイクロイド曲線に沿って振動するようにした振子をサイクロイド振子という。振幅が大きくなっても等時性を保つのが特徴である。サイクロイドの形の壁で単振子の糸の運動を制限するとサイクロイド振子になる。周期T₀の実体振子の回転軸を水平からφだけ傾けると，周期は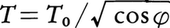，となる。φを大きくして回転軸を鉛直軸に近くすると周期が非常に長い振子を作ることができる。これを水平振子と呼び，地震計などに利用する。糸でつるしたおもりに水平面内で円運動をさせるものを円錐振子，また糸でつるしたおもりにその糸の長さを半径とする球面の上で運動させるものを円振子という。棒の先端におもりをつけた振子を逆立ちさせると不安定であるが，支点を上下方向に振動させるとおもりは小さい振幅の振動をしながら逆立ちの状態を保つ。これを倒立振子という。

　以上に説明したのはすべて重力の働きで振動する振子であるが，弾性の力で振動する振子もある。例えば上端を固定したつる巻きばねの下端におもりをつるして鉛直方向に振動させるものをばね振子という。またおもりを針金でつるし，針金をねじるように振動させるものをねじれ振子という。
執筆者：有山 正孝

図－単振子に働く力

振子 (しんし)

→振子（ふりこ）

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

振子【ふりこ】

一定の点または軸のまわりに，きまった周期をもって周期的振動を続ける物体。単振子，実体振子，水平振子，倒立振子，フーコー振子など各種ある。
→関連項目脱進機

振子【しんし】

→振子(ふりこ)

出典　株式会社平凡社

世界大百科事典（旧版）内の振子の言及

【振子】より

…ひもまたは棒の一端を支えて他端におもりをつるしたもので，固定点または固定軸のまわりで周期運動(ふつうは鉛直面内で円周に沿った振動)をする物体をいう。もっとも単純化した振子は質量がなく伸縮しないとした糸で質点をつるしたもので，これを質点振子といい，質点振子を重力の作用下で，一つの鉛直面内で振動させるものを単振子と呼ぶ。支点での摩擦も質点に対する空気抵抗も作用しないとしたとき，質点に働く力は図に示すように，重力と糸の張力で，その合力はつねに質点を円周の最下点Qに引き戻す向きに働くから，質点はQを中心として振動する。…

【ガリレイ】より

…この中で彼は，あらゆる物体が同一種類の物質から成ることを前提にしたうえで，アルキメデスの静力学的な浮力の原理を拡大することによって，落体の速度が落体の比重から媒質の比重を差し引いたものに比例すると論じている。だが，その後まもなく彼は，斜面や振子の研究を深めることによって，《運動について》では副次的役割しか与えられなかった加速度こそが，落体の運動の本質的要因であることを見抜き，ついには真空中での落下距離が落下時間の2乗に比例し，しかもそのためには落下速度が落下時間に比例しなければならないという落体の基本法則を発見した。さらにこの研究の過程で運動の合成の法則と慣性の法則を導き出し，投射体の経路がパラボラ曲線になることを証明することができた。…

【時計】より

…その中のいくつかの考案，発明は現代の時計にまで引き継がれている。その代表的なものは，振子，てんぷとひげぜんまい，アンクル脱進機である。ガリレイが振子の等時性を発見したのは1583年ころであるが，実際に精度のよい振子時計を完成したのはホイヘンスであり，1659年のことであった。…

※「振子」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」