根軸（読み）こんじく（英語表記）radical axis

精選版 日本国語大辞典

こん‐じく‥ヂク【根軸】

1. 〘 名詞 〙
2. ① 物事のおおもととなり、かなめとなるもの。根幹。
   1. [初出の実例]「総監部なるもの新設せられ、陸軍大臣に隷属し、監軍部が管掌せる各兵科の監部并に諸学校を管掌する事となりて、軍事教育の根軸を直轄すべし」(出典：国民新聞‐明治三一年（1898）一月二一日)
3. ② 数学用語。
   1. (イ) 相交わる二つの円の共通弦を含む直線。
   2. (ロ) 互いに外側にある二円の中心を結ぶ線（中心線）と共通内接線との交点で中心線に直交する直線。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

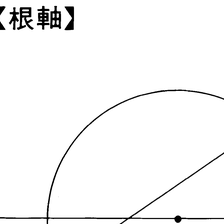
根軸 (こんじく)
radical axis

1平面上に点Pと円O（中心O）が与えられたとき，Pを通り円Oと交わる直線をとり，交点をA，Bとすれば，積PA・PBは直線のとり方によらず一定である。この値を円Oに関する点Pのべきという。平面上に2円O，O′が与えられたとき，円Oに関するべきと円O′に関するべきが等しくなる点の軌跡を2円O，O′の根軸という。円O，O′の半径をr，r′とし，中心O，O′を結ぶ直線上に点MをOM²－O′M²＝r²－r′²となるようにとれば，Mにおいて直線OO′に立てた垂線が根軸となる。2円が交わるときは2交点を結ぶ直線が根軸で，2円が接するときは接点における共通接線が根軸である。平面上に3円があり，それらの中心が1直線上にないときは，その二つずつの根軸は1点で交わる。この点を3円の根心という。平面上にいくつかの円があって，これらの二つずつの根軸がすべて同一のとき，それらの円を共軸という。
執筆者：中岡 稔

図－根軸

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

根軸
こんじく
radical axis

平面上の2円に関する方べき (方冪) の等しい点Pの軌跡を，この2円の根軸という。根軸は2円の中心を結ぶ直線 (中心線) に垂直である。いま2円の中心をそれぞれ O₁ ，O₂ ，半径をそれぞれ r₁ ，r₂ ，2円の中心線と根軸との交点を O ，根軸上の任意の1点を P とすれば，方べきの等しい点 P の軌跡は，PO₁²－r₁²＝PO₂²－r₂² ，すなわち，PO₁²－PO₂²＝OO₁²－OO₂²＝r₁²－r₂² で与えられる。2円が同心円でないかぎり根軸は存在し，2円が接しているときは，それらの共通接線，2円が交わっているときは，それらの交点を結ぶ直線がそれぞれ根軸になる。

出典　ブリタニカ国際大百科事典 小項目事典