射影平面（読み）しゃえいへいめん

日本大百科全書(ニッポニカ)

射影平面
しゃえいへいめん

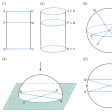
無限遠直線を付加した数学的平面をいう。射影平面は、位相的側面と、解析的側面から考察することができる。一つの線分を紐(ひも)と考え、丸めて両端を重ねれば円のように閉じる。数学のことばでは、線分の両端点を同一視すれば円と位相同形になるという。同様に図の(1)のような四角形は辺ABとDCを同一視すれば図の(2)の円柱面と位相同形になる。数学ではこのように、一つの点集合のなかのいくつかの点どうしをある法則によって同一視して新しい集合をつくることが多い。球面上で一つの直径の両端点となっている2点を互いの直径対点という。球面上の点全体のつくる点集合を考え、直径対点どうしを同一視すれば新しい集合ができる（図の(3)）。この集合を射影平面または二次元射影空間という。この場合、射影平面の構成要素（これを点とよぶ）は同一視された（普通の意味の）2点である。

　次に、球面の赤道から南を切り捨ててしまうと、残った集合は赤道上だけQとQ′、RとR′のように直径対点が同一視されている半球面である（図の(4)）。このような集合も射影平面（の一つの表現）である。この場合、北半球でQの近くの点は当然Q′に近い。この射影平面をさらに変形する。この半球を平面上に伏せて真上から平面上に正射影する。この一対一対応で平面上にできる集合は円盤（円の周も含めた内部）で、円盤上の点全体のつくる集合は、その縁(ふち)の円周上では直径対点を同一視するという条件のもとで、また射影平面の一つの表現である。図の(5)でQ、R、Q′、R′の囲む帯状の部分はQRがQ′R′に逆さに同一視されているのでメビウスの帯と位相同形である。このように射影平面はメビウスの帯を一部分として含むことから不可符号（向きづけ不可能な曲面）であることがわかる。xy平面から出発した射影平面の解析的構成法を述べる。点（x, y）に対して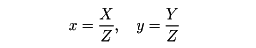

なる数X、Y、Zを対応させ、（X, Y, Z）を点（x, y）の斉次(せいじ)座標とよぶ。X：Y：Z＝X′：Y′：Z′なる（X′, Y′, Z′）も同1点の斉次座標となるから、斉次座標は比例因子を除いて定まる。いま記号（X, Y, 0）（X、Yは同時にはゼロでないとする）と記号（X′, Y′, 0）はX：Y＝X′：Y′なるとき同一視し、これらを点の仲間に入れて無限遠点とよぶことにする。もちろんこれらの新しい点はxy平面上には存在しない。X、Y、Zの一次方程式
　　(1)　　aX＋bY＋cZ＝0
を満たす点全体の集合を射影直線とよぶ。Z≠0なる(1)の解は
　　(2)　　ax＋by＋c＝0
を満たす点の全体であるから、xy平面上の直線である。Z＝0なる(1)の解は（X, Y, Z）＝（b, －a, 0）なる無限遠点である。したがって、射影直線とはxy平面上の直線に一つの無限遠点を付加したものである。(2)に平行な直線はax＋by＋c′＝0の形なので、これら平行2直線は無限遠点（b, －a, 0）で交わることがわかる。無限遠点の全体は一つの射影直線をつくる。これを無限遠直線とよぶ。xy平面に無限遠直線を付加した点集合は、距離の概念を無視して位相的に変形すれば、先に述べた射影平面になる。一般にn次元数空間の点（x₁, x₂,……, x_n）に対して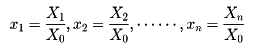

と置いて（X₁, X₂,……, X_n, X₀）を斉次座標とよべば、n＝2の場合と同様にしてn次元射影空間が構成される。

［立花俊一］

射影平面説明図〔図〕

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

射影平面 (しゃえいへいめん)
projective plane

1平面をとり，その上の各直線lに対し無限遠点と呼ぶ1点l∞を想像する。そして直線lとmが平行ならばl∞＝m∞とし，そうでなければl∞≠m∞とする。平面にこれらすべての無限遠点をつけ加えたものを射影平面という。平面に接する球をとり，接点をT，球の中心をoとして，平面上の各点pにはpとoを結ぶ直線が球面と交わる2点p′，p″を対応させ，また，Tを通る直線l上の無限遠点l∞にはoを通りlに平行な直線が球面と交わる2点l′∞，l″∞を対応させる（図1）。このようにすれば，射影平面の点とoに関して対称な球面上の2点とが対応し，したがって射影平面とは，球面において中心に関して対称な2点のおのおのをはり合わせてできる曲面ということができる。ここで，赤道を含めた北半球の点だけを考えて，これらを赤道面に正射影することにより，射影平面とは，また，円板において円周上の中心に関して対称な2点のおのおのをはり合わせてできる曲面ということができる（図2）。位相的には，さらに，射影平面は長方形で2組の対辺のおのおのを反対の向きにはり合わせてできる曲面ということもできる（図3）。射影平面は向きがつけられない曲面である。
執筆者：中岡 稔

図1～図3

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

射影平面
しゃえいへいめん
projective plane

射影空間における平面，すなわち射影空間の2次元部分空間をいう。射影座標 (斉次座標 ) を用いれば，3次元射影空間の射影平面は1つの斉次1次方程式で表わされ，n 次元射影空間の平面は，n－2 個の斉次1次方程式の組で表わされる。アフィン幾何学的にいえば，平面に無限遠直線をつけ加えた集合である。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の射影平面の言及

【射影幾何学】より

…このようにすれば，点Oからの中心射影で，m上の点は上の無限遠点にうつり，上の無限遠点はn上の点にうつって，上の点と上の点が1対1に対応し，また上の直線と上の直線が1対1に対応する。，のように平面にその上の無限遠点をつけ加えたものを射影平面といい，上で述べたからの上への1対1対応を点Oからの配景対応という。平面α,βとこれらに平行でない直線lが与えられたとき，α上の点Pに対し，その点を通りlに平行な直線がβと交わる点Qを対応させる対応(平行射影)を考えても，上の点，直線と上の点，直線に関し上と同様のことがいえる。…

【無限遠点】より

…Cに含まれる対心点の組に応ずるα上の点はないが，｛P,P^*｝がTを通る大円に沿ってC上の対心点の組に近づけばQはこの大円の面とαとの交わりである直線上をTからどんどん遠くへ離れていく(図2)。それでTを通る各直線lに対し，その上の無限の遠くに新しい1点l_∞をつくり，この点がlと平行なSの直径の両端であるC上の対心点の組に対応するとすれば，すべてのl_∞を含めたαはS上の対心点の組全体の集合，したがってS上の対心点のおのおのをはり合わせてできる曲面(これを射影平面という)と同一視でき，閉じた面となる。l_∞をlの方向の無限遠点と呼び，すべての方向の無限遠点は新しい一つの直線をつくると考えて，これを無限遠直線と呼ぶ。…

※「射影平面」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」