直交関数系（読み）ちょっこうかんすうけい（英語表記）system of orthogonal functions

改訂新版　世界大百科事典

直交関数系 (ちょっこうかんすうけい)
system of orthogonal functions

区間［a，b］で定義された2乗可積分な実数値関数f（x），g（x）に対して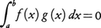，が成立するとき，f（x）とg（x）とはこの区間で直交するという。また［a，b］で定義された2乗可積分な実数値関数の列｛f_i（x）｝は，その任意の二つが直交しているとき直交関数系をなすという。直交関数系｛f_i（x）｝は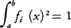，と正規化されているとき，正規直交系という。例えば区間［－π，π］で，

　1，cosx，sinx，cos2x，sin2x，……，cosnx，sinnx，……

は直交関数系であり，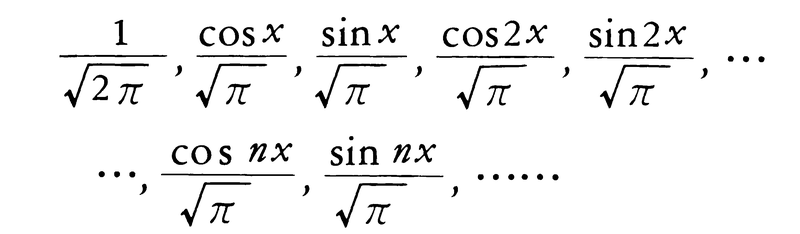

は正規直交系である。また，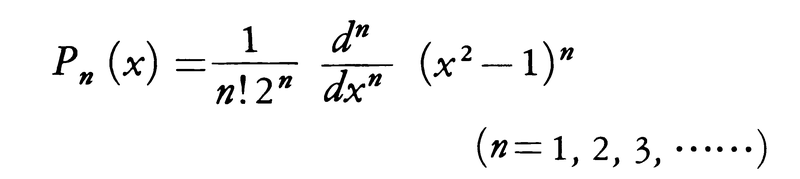

で定義されるルジャンドルの多項式は，閉区間［－1，1］において直交関数系であり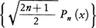，は正規直交系である。直交関数系はこれらの一次結合として関数を展開するのに用いられる。例えば，区間［－π，π］で2乗可積分な関数f（x）に対して，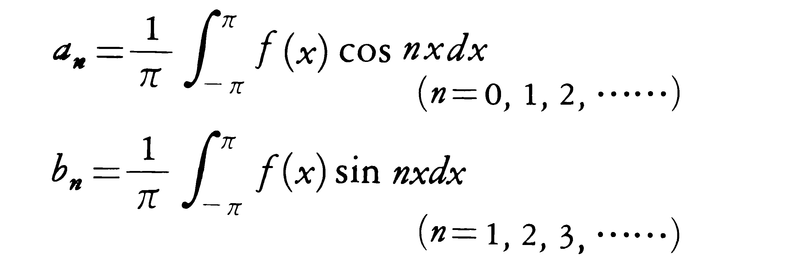

をf（x）のフーリエ係数といい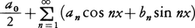，をf（x）のフーリエ展開という。この級数がいかなる条件のもとでf（x）と一致するかを調べるのはフーリエ級数論のたいせつな問題である。例えば，f（x）が閉区間［－π，π］で連続，f（－π）＝f（π）かつ微分可能でその導関数も連続であれば，f（x）のフーリエ展開は［－π，π］で一様絶対収束しf（x）と一致する。

　直交関数系はヒルベルト空間の理論でもたいせつな役割をはたしている。
執筆者：上野 健爾

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

直交関数系
ちょっこうかんすうけい
orthogonal system of function

区間 [－π，π] で定義された関数列を1， cos x ， sin x ， cos 2x ， sin 2x ，…， cos nx ， sin nx ，…とする。これらの関数は，どの2つをとっても，互いに直交している。このように，ある定まった区間 [a，b] で定義された関数列 {f(x)} において，これらのうちの任意の2つが直交しているとき，それらは [a，b] における直交関数系，あるいは単に直交系と呼ばれる。

出典　ブリタニカ国際大百科事典 小項目事典