直和 (ちょくわ)
direct sum
数学用語。
集合の直和
一つの集合Mが共通部分をもたない部分集合A,Bの和集合のとき,MはAとBの直和であるという。共通元をもつかもしれない二つの集合A,Bについて,Aと1対1対応をもつ集合A′を作って,A′とBが共通元をもたないようにして,A′∪Bを作り,これもAとBの直和といい,A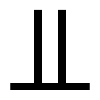 Bで表す。多くの集合についても同様に考える。
Bで表す。多くの集合についても同様に考える。
加法群,または環の直和
G1,G2が加法群,または環のとき,集合としての直積G1×G2={(a,b)|a∈G1,b∈G2}に(a,b)+(a′,b′)=(a+a′,b+b′)で加法を定義し,環のときはさらに(a,b)(a′,b′)=(aa′,bb′)で乗法を定義すれば,G1×G2も加法群,または環になる。これをG1とG2の直和といい,G1⊕G2で表す。{Gλ}λ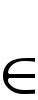 Λが加法群の集りのときには,{Gλ}の直積集合の部分集合{(……,aμ,……,aλ,……)|有限個のλを除いてaλ=0}に(……,aμ,……,aλ,……)+(……,bμ,……,bλ,……)=(……,aμ+bμ,……,aλ+bλ,……)で加法を定めたものを直和といい,これを
Λが加法群の集りのときには,{Gλ}の直積集合の部分集合{(……,aμ,……,aλ,……)|有限個のλを除いてaλ=0}に(……,aμ,……,aλ,……)+(……,bμ,……,bλ,……)=(……,aμ+bμ,……,aλ+bλ,……)で加法を定めたものを直和といい,これを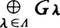 で表す。環の集りの場合も同様である。
で表す。環の集りの場合も同様である。
執筆者:丸山 正樹
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
直和
ちょくわ
direct sum
(1) 集合に関して 集合 A と B との和集合というときに,A ,B⊆X の場合の合併をさす場合もあるが,A と B を重なりを考えずに並べたものをいう場合もある。これを合併集合と区別するために直和ということもある。転じて,部分集合の合併についても,A∩B=φ の場合に限って直和ということもある。 (2) 可換群に関して 加法に関する結合法をもつ可換群を G ,その部分群を G1 ,G2 とする。もし任意の元 x∈G ,x1∈G1 および x2∈G2 によって,x=x1+x2 の形に一意的に書けるとき,G は G1 と G2 の直和であるといわれ,これを G1+G2 で表わす。 (3) ベクトル空間に関して ベクトル空間の算法は加法なので,直積のことを直和ということもある。 (4) ベクトル空間の部分空間に関して 体 K の上のベクトル空間を V ,その部分空間を V1 ,V2 とする。もし V のおのおの元 x が,x1∈V1 および x2∈V2 によって,一意的に x=x1+x2 と書けるとき,V は V1 と V2 の直和であるといい,これを V1+V2 で表わす。一般にも,V1+V2={x1+x2|x1∈V1,x2∈V2} と書くが,これは V1 と V2 の直和 (直積) と同型とはかぎらない。それで特に,同型になる場合を直和というのである。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
世界大百科事典(旧版)内の直和の言及
【直積】より
…すべてのAλが単位元をもつときは,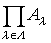 も単位元をもつ。{Aλ}λ∈Aの加法群としての制限直積は
も単位元をもつ。{Aλ}λ∈Aの加法群としての制限直積は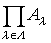 の部分環となり,{Aλ}λ∈Aの直和ともいわれる。【丸山 正樹】。…
の部分環となり,{Aλ}λ∈Aの直和ともいわれる。【丸山 正樹】。…
※「直和」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by 
 Bで表す。多くの集合についても同様に考える。
Bで表す。多くの集合についても同様に考える。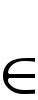 Λが加法群の集りのときには,{Gλ}の直積集合の部分集合{(……,aμ,……,aλ,……)|有限個のλを除いてaλ=0}に(……,aμ,……,aλ,……)+(……,bμ,……,bλ,……)=(……,aμ+bμ,……,aλ+bλ,……)で加法を定めたものを直和といい,これを
Λが加法群の集りのときには,{Gλ}の直積集合の部分集合{(……,aμ,……,aλ,……)|有限個のλを除いてaλ=0}に(……,aμ,……,aλ,……)+(……,bμ,……,bλ,……)=(……,aμ+bμ,……,aλ+bλ,……)で加法を定めたものを直和といい,これを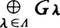 で表す。環の集りの場合も同様である。
で表す。環の集りの場合も同様である。

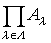 も単位元をもつ。{Aλ}λ∈Aの加法群としての制限直積は
も単位元をもつ。{Aλ}λ∈Aの加法群としての制限直積は