直積（読み）ちょくせき（英語表記）direct product

精選版 日本国語大辞典

ちょく‐せき【直積】

〘名〙 集合ＡとＢに対して、Ａの要素ａとＢの要素ｂを組にした (a, b) の形のもの全体の作る集合をいう。ＡとＢの直積は、A×B で表わされる。積集合。

じき‐づみ ヂキ‥【直積】

〘名〙 (prompt shipment の訳語) 契約成立の日から、二週間以内に船積みを完了すること。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

直積 (ちょくせき)
direct product

二つの集合A₁，A₂が与えられたとき，A₁の元とA₂の元の組の集合｛（a₁，a₂）｜a₁∈A₁，a₂∈A₂｝をA₁とA₂の直積集合といい，A₁×A₂で表す。各（a₁，a₂）∈A₁×A₂にa_i∈A_i（i＝1，2）を対応させる写像p_iをA₁×A₂からA_iへの射影という。より一般に集合Λで添字づけられた集合の集り｛A_λ｝_λ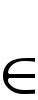Λについて，集合｛（……，a_μ，……，a_λ，……）｜a_λ∈A_λ｝を｛A_λ｝_λ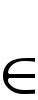Λの直積とよんで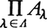，で表す。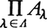から各A_λへの射影p_λも二つの集合のときと同様に定める。各A_λが群のとき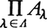の積を（……，a_μ，……，a_λ，……）（……，b_μ，……，b_λ，……）＝（……，a_μb_μ，……，a_λb_λ，……）で定めれば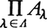は群になり，各p_λは群の準同型である。 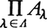の部分集合 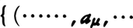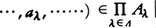有限個のλを除いてa_λは単位元｝は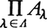の正規部分群となる。これを｛A_λ｝_λ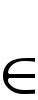Λの制限直積という。各A_λが環のとき，（……，a_μ，……，a_λ，……）＋（……，b_μ，……，b_λ，……）＝（……，a_μ＋b_μ，……，a_λ＋b_λ，……），（……，a_μ，……，a_λ，……）（……，b_μ，……，b_λ，……）＝（……，a_μb_μ，……，a_λb_λ，……）で算法を定めれば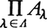は環になる。すべてのA_λが単位元をもつときは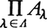，も単位元をもつ。｛A_λ｝_λ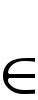Λの加法群としての制限直積は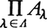，の部分環となり，｛A_λ｝_λ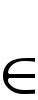Λの直和ともいわれる。
執筆者：丸山 正樹

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

直積
ちょくせき
direct product

最近では単に積 product ということも多い。 (1) 集合に関して　2つの集合 A ，B に対して，a∈A ，b∈B であるあらゆる a ，b の組 (a，b) によってつくられる集合を A と B の積，直積あるいは積集合といい，A×B で表わす。すなわち内包的記法で書けば，A×B＝{(a，b)｜a∈A，b∈B} である。また一般に n 個の集合 A₁ ，A₂ ，…，A_n に対して Π_i=1ⁿA_i＝A₁×A₂×…×A_n＝{(a₁，a₂，…，a_n)｜a₁∈A₁，a₂∈A₂，…，a_n∈A_n} を，それらの集合の直積と定義する。無限個の集合に対しても，同様に定義することができる。 (2) 群に関して　 G₁ ，G₂ を群とし，x₁∈G₁ ，x₂∈G₂ であるすべての対 (x₁，x₂) の集合を G₁×G₂ とする。いま (x₁，x₂) および (x'₁，x'₂) を G₁×G₂ の元とするとき，これら2元の積を (x₁x'₁，x₂x'₂) なる対と定義すれば，G₁×G₂ はまた群となる。こうして群の構造を与えられた G₁×G₂ を G₁ と G₂ の積あるいは直積と呼ぶ。一般に集合 A ，B が代数的構造をもつ場合は，A×B にも同じ代数的構造を与えることができれば，その A×B を A と B の積あるいは直積という。 (3) ベクトル空間に関して　 V₁ ，V₂ を任意のベクトル空間，v₁∈V₁ ，v₂∈V₂ である，すべての対 (v₁，v₂) の集合を V₁×V₂ とする。いま，2つの対 (v₁，v₂) および (v'₁，v'₂) をともに V₁×V₂ の元とするとき，和を (v₁，v₂)＋(v'₁，v'₂)＝(v₁＋v'₁，v₂＋v'₂) ，また体 K の任意の元 a に対して，積を c(v₁，v₂)＝(cv₁，cv₂) と定義すれば，V₁×V₂ はまたベクトル空間になる。このとき V₁×V₂ を V₁ と V₂ の直積と呼ぶ。

出典　ブリタニカ国際大百科事典 小項目事典

日本大百科全書(ニッポニカ)

直積
ちょくせき

A、Bを二つの集合とする。

　　(x,y),x∈A,y∈B
という形式の全体Cを考え、
　　(x,y)=(x′,y′)⇔x=x′,y=y′
と定義する。このときCを集合AとBの直積といい、A×Bと記す。たとえば、実数直線をRとするとき、平面はR×Rと考えられる。これが座標平面の考え方である。三つ以上の集合の直積も同様に考えられる。

　さらに、A_λ　(λ∈Λ)を集合の族（集まり）とする。形式
　　(x_λ)_λ∈Λ,　x_λ∈A
　　　(λ∈Λ)
の全体を考えて、A_λ　(λ∈Λ)の直積といい、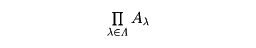

と記す。もちろん、
　　(x_λ)_λ∈Λ=(y_λ)_λ∈Λ
　　　⇔x_λ=y_λ　(λ∈Λ)
とする。

　直積は公理的集合論において厳密に定義される。写像の概念は直積の概念から定義されるのが普通である。とくにA、Bが群（他の代数系でもよい）であるとする。(x₁,y₁),(x₂,y₂)を直積A×Bの二元とするとき
　　(x₁,y₁)・(x₂,y₂)=(x₁x₂,y₁y₂)
により積を定義するならば、A×Bはふたたび群となる。これを群A、Bの直積という。とくにA、Bが加群のときは直和とよばれ、A⊕Bのように記されることが多い。

［足立恒雄］

出典　小学館　日本大百科全書(ニッポニカ)

世界大百科事典（旧版）内の直積の言及

【集合】より

…ここで，集合算というのは，∩，∪を集合間の演算と考えたことをいうのである。
［直積］
　二つの集合A,Bが与えられたとき，Aの元とBの元の組の集合｛(a,b)｜a∈A,b∈B｝をAとBの直積(または直積集合)といい，A×Bで表す。これは集合｛1,2｝から，A∪Bの中への写像fで，f(1)∈A,f(2)∈Bを満たすものの全体Tを取ると，Tの元fとA×Bの元(f(1)，f(2))との対応によって，TとA×Bとの1対1対応が得られる。…

※「直積」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」