面積分 (めんせきぶん)
surface integral
xyz空間で滑らかな曲面Sが媒介変数u,vによりx=x(u,v),y=y(u,v),z=z(u,v)(α≦u≦β,γ≦v≦δ)と表されているとする。ここで,
E=(xu)2+(yu)2+(zu)2
F=xuxv+yuyv+zuzv
G=(xv)2+(yv)2+(zv)2
(ただし,例えばxu,xvは∂x/∂u,∂x/∂vを表す)
とおくと,曲面Sの上での面積要素は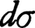
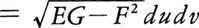 で与えられる。f(x,y,z)をS上で定義された連続関数とし,
で与えられる。f(x,y,z)をS上で定義された連続関数とし,
g(u,v)≡f(x(u,v),y(u,v),
z(u,v))
とおく。このとき,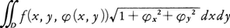 と定義し,これをfのS上での面積分という。とくに曲面Sがz=φ(x,y)((x,y)∈D)で与えられているときは,この面積分は,
と定義し,これをfのS上での面積分という。とくに曲面Sがz=φ(x,y)((x,y)∈D)で与えられているときは,この面積分は,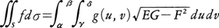 で与えられる。
で与えられる。
執筆者:伊藤 清三
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
面積分
めんせきぶん
surface integral
三次元空間において、曲面x=x(u,v),y=y(u,v),z=z(u,v)が与えられたとして、この曲面を含む空間内の一つの領域Dにおいて定義された連続関数f(x,y,z)があるとき、これをこの曲面上で積分することを考える。
いま、u、vがu‐v平面内のある領域Mを動くとき、対応して曲面上の部分SMが描かれるものとする。Mを細かい網目(あみめ)に分割し(平面上の面積を考えたときのように)、対応して得られる曲面上の小部分Skと、Sk内の一点Pkをとって、Σf(Pk)Skを考えると、これは網目を一様に細かくしていくとき、ある極限値に収束する。この値をf(x,y,z)の曲面SM上における面積分といって、
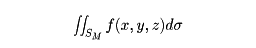
で表す。次に、
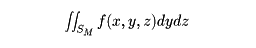
という形の面積分を定義する。そのために、この曲面の各点における単位法線ベクトルをn=(λ,μ,ν)とする。そして
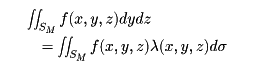
と定める。dzdx,dxdyに関する積分は、λをそれぞれμ、νで置き換えたものとする。
[竹之内脩]
空間内の有界な領域DでC1級関数(連続な偏導関数を有する関数)f(x,y,z)が与えられているとする。D内に、閉曲面Sによって囲まれた部分領域Vを考えるとき、
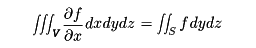
などが成り立つ。
これは、線積分の場合のグリーンの公式に対応するものであり、重積分の計算において重要である。また、ストークスの定理とよばれる定理も著名でよく用いられる。
[竹之内脩]
出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例
Sponserd by 
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
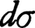
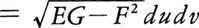 で与えられる。f(x,y,z)をS上で定義された連続関数とし,
で与えられる。f(x,y,z)をS上で定義された連続関数とし,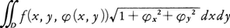 と定義し,これをfのS上での面積分という。とくに曲面Sがz=φ(x,y)((x,y)∈D)で与えられているときは,この面積分は,
と定義し,これをfのS上での面積分という。とくに曲面Sがz=φ(x,y)((x,y)∈D)で与えられているときは,この面積分は,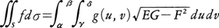 で与えられる。
で与えられる。

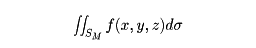
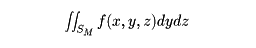
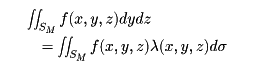
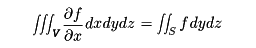
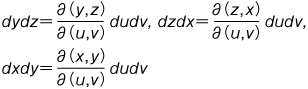 が考えられるので,微分式 Fdydz+Gdzdx+Hdxdy に対して,
が考えられるので,微分式 Fdydz+Gdzdx+Hdxdy に対して,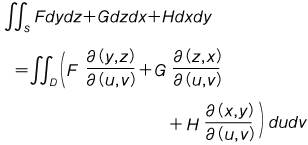 として,この微分式の積分が考えられる。これをこの微分式の S の上での面積分という。また
として,この微分式の積分が考えられる。これをこの微分式の S の上での面積分という。また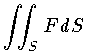 を考えることができる。特に
を考えることができる。特に 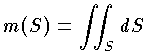 が,曲面 S の面積である。
が,曲面 S の面積である。