重積分（読み）じゅうせきぶん

精選版 日本国語大辞典

じゅう‐せきぶんヂュウ‥【重積分】

1. 〘 名詞 〙 定積分の概念を変数に拡張したもの。多重積分。〔数学ニ用ヰル辞ノ英和対訳字書（1889）〕

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

重積分
じゅうせきぶん

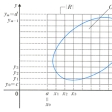
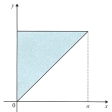
多変数の関数を積分する方法。以下、2変数の場合について説明する。図Aのようにxy平面上の、座標軸に平行な辺をもつ長方形Rを考える。

　　R : a≦x≦b, c≦y≦d
このような長方形の面積(b－a)(d－c)を以下、|R|で表す。そして、Rに含まれるような図形Gについて、Gの面積を定めよう。いま、区間［a, b］［c, d］を任意に細分して、その分点を順に次のようにする。

　　a＝x₀＜x₁＜x₂＜……＜x_n＝b
　　c＝y₀＜y₁＜y₂＜……＜y_m＝d
これによって、Rはnm個の小長方形に分割されるが、これらの小長方形のうち、Gにすっかり含まれてしまうものをR₁, R₂,……, R_pとし、Gと少なくとも1点を共有するものをR₁, R₂,……, R_p, R_p+1,……, R_p+qとする。Rの分割を一つ定めると、|R₁|＋|R₂|＋……＋|R_p|が定まるが、分割をいろいろ変えて得られるこの値の上限を、Gの内側の面積、あるいはジョルダンの内測度、またはジョルダンの内容量という。これはすなわち、分割の大きさを細かくしていったときの、|R₁|＋|R₂|＋……＋|R_p|の極限値である。同様に、各分割において定まる|R₁|＋R₂|＋……＋|R_p|＋|R_p+1|＋……＋|R_p+q|の値の、分割をいろいろ変えたときの下限を、Gの外側の面積、ジョルダンの外測度、ジョルダンの外容量などとよぶ。外側の面積と内側の面積が一致するとき、Gは面積確定であるといい、この共通の値をGの面積という。

　Gは平面上のある長方形に含まれた面積確定な集合であるとし、この集合の上で、有界な関数f(x, y)を積分することの意味を次のように定める。すなわち、Rを細分し、その分割の小長方形のうちGに含まれるものR₁, R₂,……, R_pについて、(a_k, b_k)をR_k内の1点として、和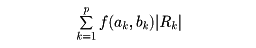

をつくる。これはfのグラフとxy平面で囲まれる図形を、底面積|R_k|、高さf(a_k, b_k)の小直方体の集まりで近似したときの、近似図形の体積にほかならない。分割をいろいろに変え、また、各小長方形内で点(a_k, b_k)のとり方をいろいろに変えるとき、どのようにしても、分割の大きさを小さくしていくと、その極限において、つねに一定の値Aに近づくならば、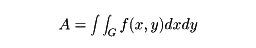

と表し、これをf(x, y)のG上の二重積分という。または単にf(x, y)のG上の積分という。右辺は象徴的に、横dx、縦dyなる微小長方形を底面にもつ、高さf(x, y)の直方体の体積（高さ×底面積＝f(x, y)dxdy）の無限和をとることを表している。f(x, y)のG上の積分が存在するとき、f(x, y)はG上で積分可能であるという。有界連続関数は、つねに積分可能である。通常の1変数の定積分は、y＝f(x)のグラフとx軸との間に挟まれた部分の面積を表すものであった。同様に、重積分は、z＝f(x, y)のグラフとして得られる曲面とxy平面との間の、Gの上に立てた柱状部分の体積を表すことは、以上の定義により直観的には明らかであろう。

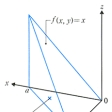
〔例1〕f(x, y)＝xとし、Gを原点とx軸上x＝aの点、およびy軸上y＝aの点を結ぶ三角形の内部とするとき、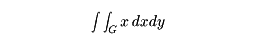

は、図Bのプリズム形の体積を与える（計算の方法については後に示す）。

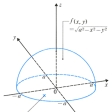
〔例2〕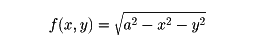

とし、Gをxy平面内の円x²＋y²＝a²の内部とすれば、定積分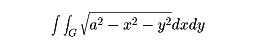

は半球の体積である（図C）。

［竹之内脩］

繰り返し積分

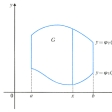
重積分はこのように定義されたが、その値を求めるのには、そのままでは困難であるので、1変数の積分の繰り返しに変形する。いま、積分の範囲Gが、区間［a, b］で定義された連続な関数₁(x), ₂(x)（₁(x)＜₂(x)とする）によって、2直線x＝a, x＝bと、曲線y＝₁(x), y＝₂(x)によって囲まれた図形であるとする（図D）。そうすると、

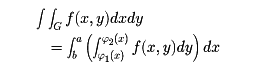
のように、重積分の値は1変数の積分を繰り返すことによって求められる。

　〔例1〕の場合、Gは、0≦x≦aで、y＝0とy＝a－xで囲まれた三角形である。ゆえに、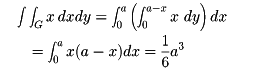

　〔例2〕の場合には、Gは、－a≦x≦aで、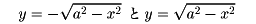

で囲まれた円である。ゆえに、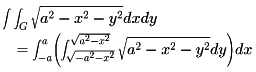

内側の積分は、半径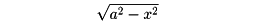

の上半円の面積を表すことになるから、その値は(π/2)(a²－x²)ゆえに、この積分は、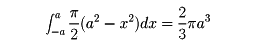

［竹之内脩］

積分順序の変更

重積分を繰り返し積分の形にするには、yについて積分してからxについて積分する、xについて積分してからyについて積分する、という二つの方向がある。これを逆に利用すれば、初めに繰り返し積分が与えられたとき、この積分の順序を変更することができる。例について説明しよう。

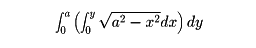
の場合、この内側のxに関する積分は、求められないことはないが、ずいぶんめんどうな形となる。そこで、積分の順序を変更し、yに関する積分を先に行う。このとき、積分範囲Gは図Eのような形であるから、それに注意すると、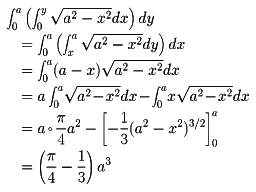

として、比較的容易に求められることになる。

［竹之内脩］

重積分における変数変換

重積分において積分変数の変換をするときは、ヤコビアンを用いて、次のようにする。x＝(u, v), y＝ψ(u, v)によって、x、yからu、vに変数変換をし、そのときに、積分の範囲Gが、uv平面のHに変わったとすれば、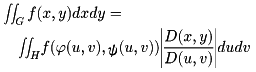

ここで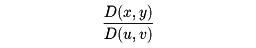

はヤコビアンである。

　〔例2〕において、x＝rcosθ,y＝rsinθと極座標に変換すれば、Hは、0≦r≦a, 0≦θ≦2πとなり、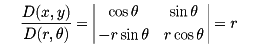

であるから、次のようになる。

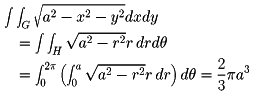
　重積分について、以上の方法はリーマン積分の行き方である。この方法で一般論を展開するのには、いろいろ困難が多い。ルベーグ積分によるならば、甚だ明快な答えが得られる。ルベーグ積分において、重積分と繰り返し積分の関係を述べたものを、フビニの定理という。

［竹之内脩］

[参照項目] | リーマン積分 | ルベーグ積分

重積分説明図〔図A〕

重積分（例1）〔図B〕

重積分（例2）〔図C〕

重積分（繰り返し積分）〔図D〕

重積分（積分順序の変更）〔図E〕

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

重積分 (じゅうせきぶん)
multiple integral

多変数の関数の多変数の範囲にわたる積分を重積分または重複積分という。1変数の関数の積分を単一積分というのに対応してつけられた名称である。例えば，xy平面上の領域Eの上で定義された関数f（x，y）の，Eにおける二重積分（2変数に関する重積分）は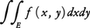と記される。とくにEが長方形a≦x≦b，c≦y≦dのとき，f（x，y）が適当な条件を満たせば（例えばf（x，y）がEで連続ならば），二重積分は単一積分の反復の形に書き直すことができる。すなわち，

ここで（1），（2）の表記法はそれぞれ，

の意味であって，この形の積分を累次積分という。二重積分の変数変換については次の事実が成り立つ。x＝φ（u，v），y＝ψ（u，v）により，uv平面上の有限個の滑らかな曲線で囲まれた領域Bからxy平面上の同様な領域Aへの写像が与えられ，この対応が1対1であってφ，ψは連続微分可能な関数とする。

いま行列式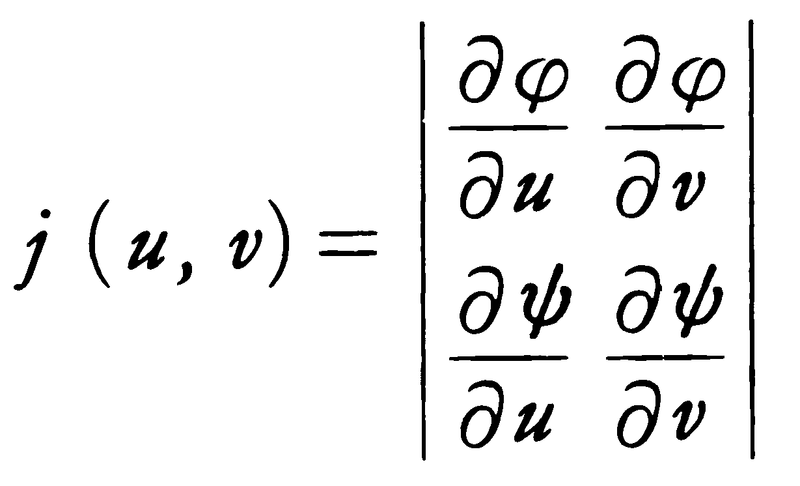

がBにおいて0にならないならば，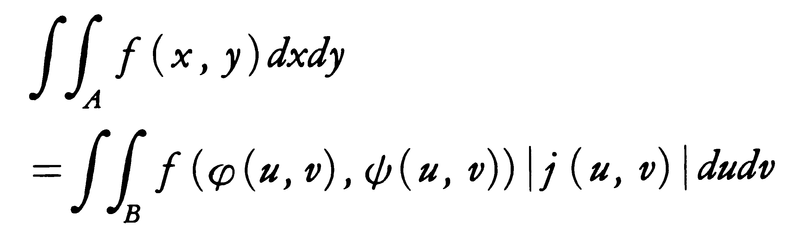

これは1変数の置換積分の公式に相当している。
→積分
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

重積分
じゅうせきぶん
multiple integral

多重積分ともいう。重積分には，二重積分，三重積分，…，一般に n 重積分がある。二重積分について述べよう。2次元数空間の面積確定の閉領域 D 上で，関数 f(x，y) が定義されているとき，D を任意の方法で，n 個の重なり合わない閉領域 ΔD₁，ΔD₂，…，ΔD_n に細分し，D の点を含む各 ΔD_i(i＝1，2，…，n) に D の任意の点 (x₁，y₁) をとって，このような ΔD_i に対する和
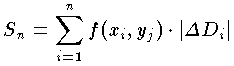をつくる。ここで ｜ΔD_i｜ は ΔD_i の面積である。いま n を限りなく大きくして分割の幅を0に近づけるとき，領域 D の分割の仕方や各 ΔD_i における点 (x_i，y_i) のとり方にまったく無関係に S_n が有限な極限値に近づくならば，f(x，y) は，閉領域 D において積分可能であるといい，この極限値を，f(x，y) の D における二重積分と呼び
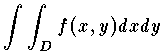で表わす。 f(x，y) が D 上で連続であれば，f(x，y) は D において積分可能である。二重積分の考え方を，同じような方法で拡張して三重積分，一般には n 重積分を定義することができる。

出典　ブリタニカ国際大百科事典 小項目事典