日本大百科全書(ニッポニカ) 「線積分」の意味・わかりやすい解説
線積分
せんせきぶん
曲線に沿って行う積分のことで、曲線積分ともいう。いま、Lは2点A、Bを結ぶ長さのある曲線とする。L上での関数f(P)の線積分
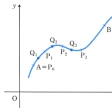
を次のように定める。A、Bの間の曲線の部分に順に数多くの点P1,P2,……,Pn-1(A=P0,B=Pnとする)をとり、またP0,P1の間に点Q1、P1,P2の間に点Q2、……、Pn-1,Pnの間に点Qnをとり()、和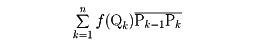
を考える。ここで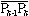 は、Pk-1,Pkを結ぶ線分の長さである。点P1,P2,……,Pn-1,Q1,Q2,……,Qnのとり方をいろいろに変えるとき、どのようにそれらをとっても、これらの点をL上密になるようにしていったとき、ある極限値に収束するならば、この極限値を前記線積分(*)の値と定義する。f(P)がLを含むような平面のある部分において有界連続ならば、線積分は存在する。線積分の近似和において、
は、Pk-1,Pkを結ぶ線分の長さである。点P1,P2,……,Pn-1,Q1,Q2,……,Qnのとり方をいろいろに変えるとき、どのようにそれらをとっても、これらの点をL上密になるようにしていったとき、ある極限値に収束するならば、この極限値を前記線積分(*)の値と定義する。f(P)がLを含むような平面のある部分において有界連続ならば、線積分は存在する。線積分の近似和において、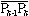 を、たとえば、各点のx座標の差xk-xk-1で置き換えて、
を、たとえば、各点のx座標の差xk-xk-1で置き換えて、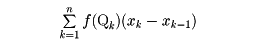
を考え、これの極限値として線積分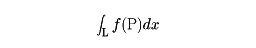
が定義される。同様に、線積分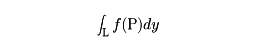
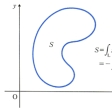
も定められる。たとえば、平面上の長さのある単純閉曲線Lで囲まれた部分()の面積をSとすれば、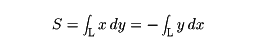
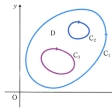
平面上の有界な領域Dの境界が、区分的に滑らかな有限個の単純閉曲線C1,C2,……,Cmからなるとする()。これらの境界の曲線は、すべてDの内部を左側に見ながら回る向きをつけてあるものとし、まとめてCで表す。いま、f(x,y),g(x,y)が、D上境界も含めた範囲でC1級関数(連続な偏導関数を有する関数)ならば、次の式が成立する。
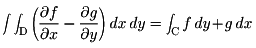
これをグリーンの定理という。
[竹之内脩]
複素関数の線積分
線積分の近似和における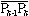 を、各点を表す複素数の差zk-zk-1で置き換えて
を、各点を表す複素数の差zk-zk-1で置き換えて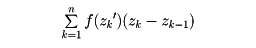
(Zk′はQkに対応する複素数)とし、これの極限値として、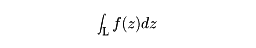
が定義される。コーシーの積分定理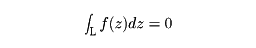
および、コーシーの積分公式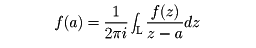
などは、この線積分を用いたものである。
[竹之内脩]


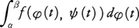 を,fのCに沿ってのxに関する線積分といい,
を,fのCに沿ってのxに関する線積分といい,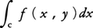 または単に,
または単に,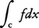 と書く。同様にfのyに関する線積分,
と書く。同様にfのyに関する線積分,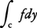 も定義される。とくにφ(t)が連続微分可能なら,
も定義される。とくにφ(t)が連続微分可能なら,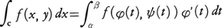 となって,ふつうの積分の
となって,ふつうの積分の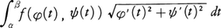 をfのCに沿っての線素に関する線積分といい,
をfのCに沿っての線素に関する線積分といい,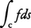 と書く。n次元空間における曲線,
と書く。n次元空間における曲線,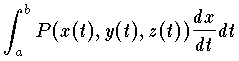 が存在するならば,これを C に沿う P(x,y,z) の x に関する線積分といい,
が存在するならば,これを C に沿う P(x,y,z) の x に関する線積分といい,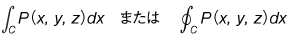 と書く。
と書く。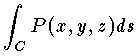 が定義できる。特に
が定義できる。特に 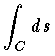 はこの曲線 C の長さになる。
はこの曲線 C の長さになる。