改訂新版 世界大百科事典 「収束半径」の意味・わかりやすい解説
収束半径 (しゅうそくはんけい)
convergence radius
a0,a1,a2,……を複素数の定数,zを複素数の変数とするとき,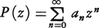 の形の級数をべき級数という。べき級数P(z)がz=z0で収束すれば|z|<|z0|なるすべてのzに対して絶対収束する。このような|z0|の上限をRとすると,P(z)は|z|<Rなるすべてのzで絶対収束し,|z|>Rなるすべてのzで発散する。このようなRをべき級数P(z)の収束半径という。P(z)がz=0以外で発散するときはR=0とする。収束半径を求める公式として
の形の級数をべき級数という。べき級数P(z)がz=z0で収束すれば|z|<|z0|なるすべてのzに対して絶対収束する。このような|z0|の上限をRとすると,P(z)は|z|<Rなるすべてのzで絶対収束し,|z|>Rなるすべてのzで発散する。このようなRをべき級数P(z)の収束半径という。P(z)がz=0以外で発散するときはR=0とする。収束半径を求める公式として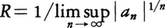 (lim supは上極限)がある。ただし1/∞=0,1/0=∞とする。これをコーシー=アダマールの公式という。なお,もしも
(lim supは上極限)がある。ただし1/∞=0,1/0=∞とする。これをコーシー=アダマールの公式という。なお,もしも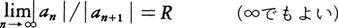 が存在すれば,これが収束半径である。例えば,
が存在すれば,これが収束半径である。例えば,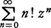 についてはR=0,
についてはR=0,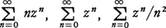 については,いずれもR=1,
については,いずれもR=1,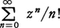 についてはR=∞。
についてはR=∞。
執筆者:伊藤 清三
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報


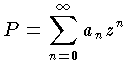 が z=z0 で収束すれば,P は |z|<|z0| であるすべての z について収束する。このような値 |z0| の上界 ζ を収束半径といい,円周 ρ=|z| または円の
が z=z0 で収束すれば,P は |z|<|z0| であるすべての z について収束する。このような値 |z0| の上界 ζ を収束半径といい,円周 ρ=|z| または円の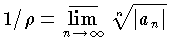 で与えられる。
で与えられる。