改訂新版 世界大百科事典 「Γ関数」の意味・わかりやすい解説
関数 (ガンマかんすう)
gamma function
解析学で重要な特殊関数。1929年，L.オイラーは定積分に関連して，次の無限乗積を複素数zに対し導入した。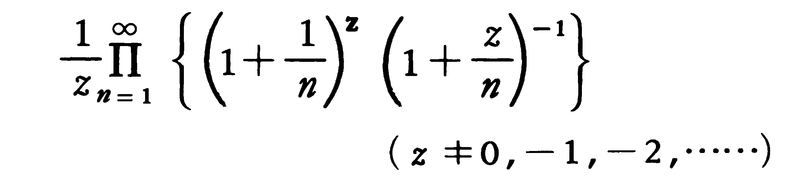
これをA.M.ルジャンドルが，ガンマ関数と命名し，記号Γ（z）を用いた。上の式は，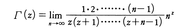
と一致するが，さらに書き直せば，次のワイヤーシュトラスの標準形に変形できる。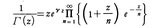
ここに，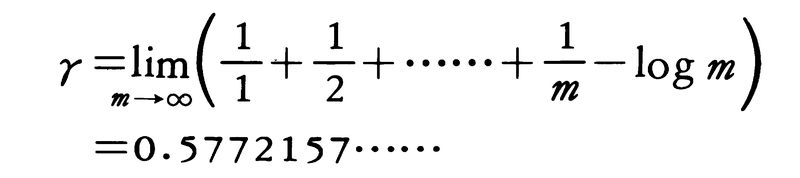
は，オイラーの定数である。ワイヤーシュトラスの標準形からわかるように，Γ関数はz＝0，－1，－2，……で1位の極をもち，その他では解析的になる。Γ関数に対し次の方程式が成り立つ。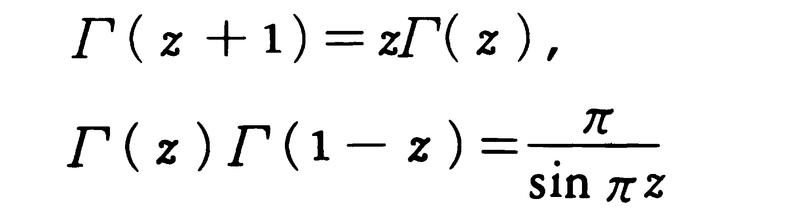
したがって，Γ（1）＝1を用いると，正整数nに対しΓ（n＋1）＝n！。また，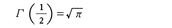
である。第2種のオイラー積分
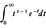は，zの実部か正となる半平面で正則関数になるが，積分値はΓ（z）に等しい。第1種のオイラー積分，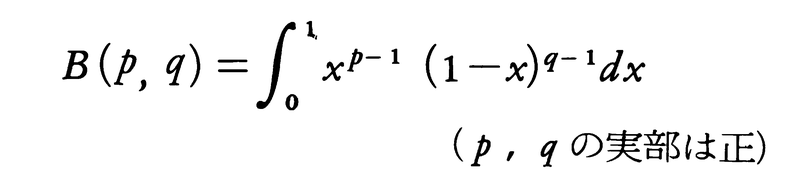
はベータ関数と呼ばれ，Γ関数を用いて，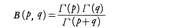
と表される。xが大きな正の数のとき，Γ（x）の近似値を求めるのに，次の漸近展開（スターリングの公式）は有用である。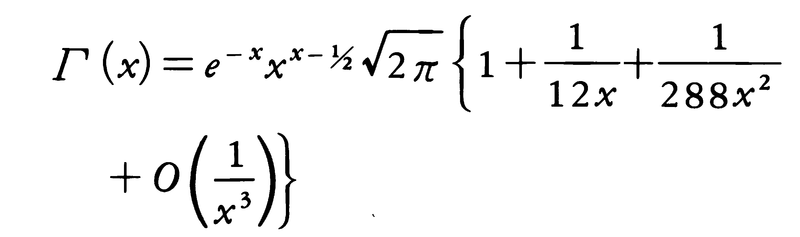
執筆者：西尾 真喜子
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 