特殊関数（読み）とくしゅかんすう

日本大百科全書(ニッポニカ)

特殊関数
とくしゅかんすう

解析学やその応用分野でしばしば現れる関数や関数族を通常特殊関数と総称している。ただし指数関数、三角関数のような初等関数はこれに含ませないことが多い。ガンマ関数、ベータ関数、ベッセル関数、ルジャンドルの多項式、球関数、直交関数系、楕円(だえん)積分などは特殊関数である。

［小林良和］

ベッセル関数

ベッセルの微分方程式
　　x²y″+xy′+(x²-ν²)y=0
の解をベッセル関数という。この解のうち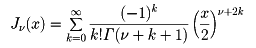

をν次の第1種ベッセル関数という。これと独立な解
　　N_ν(x)=｛(cosνπ)J_ν(x)-J_-ν(x)｝/sinνπ
をν次の第2種ベッセル関数またはノイマン関数とよぶ。ただしν=nが整数のときはν≠nをnに近づけたときの極限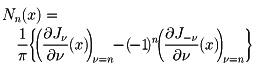

でN_n(x)を定義する。ベッセルの微分方程式の基本解系としては
　　H_ν⁽¹⁾(x)=J_ν(x)+iN_ν(x),
　　H_ν⁽²⁾(x)=J_ν(x)-iN_ν(x)
も使われる。

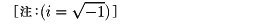
これらを第3種ベッセル関数またはハンケル関数という。nが整数のときJ_n+1/2(x)は初等関数で表され、たとえば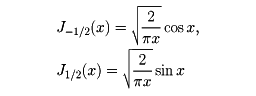

である。nを非負整数、l＞0とする。このときJ_n(lx)は可算無限個の零点をもつ。これをλ₁＜λ₂＜……＜λ_k＜……と置くと、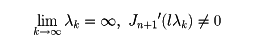

が成り立ち、関数列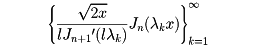

は区間(0,l)において完備な正規直交系になる。

［小林良和］

ルジャンドルの多項式

n次の多項式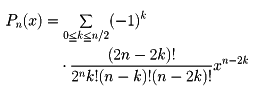

をn次のルジャンドルの多項式という。これはルジャンドルの微分方程式
　　(1-x²)y″-2xy′+n(n+1)y=0
を満たす。この方程式はP_n(x)と独立な解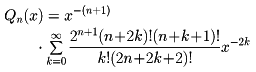

をもつ。これを第2種ルジャンドル関数といい、これに対しP_n(x)を第1種ルジャンドル関数という。

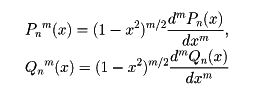
をそれぞれ第1種、第2種のルジャンドル陪関数とよび、これらはルジャンドルの陪微分方程式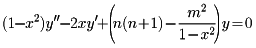

の独立な解を与える。mを固定すると、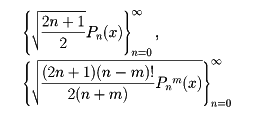

はそれぞれ区間（-1,1）で完備な正規直交関数系になる。

［小林良和］

球関数

三次元のラプラス方程式の解で直交座標x、y、zに関しn次の同次関数であるものをn次の体球関数という。極座標r、θ、を用いるとn次の体球関数はrⁿY(θ,)と書けるが、このY_n(θ,)をn次の球面関数という。これらの関数を総称して球関数という。球面関数は微分方程式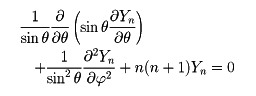

を満たす。nを正整数とし、この変数分離形の解を求めると、P_n(x),P_n^m(x)をそれぞれ第1種のルジャンドル関数と陪関数として2n+1個の独立な解
　　P_n(cosθ),
　　P_n^m(cosθ)cosm,
　　P_n^m(cosθ)sinm
　　m=1,2,……,n
を得る。これらのうち最初のものを帯球関数、そのほかを縞(しま)球関数という。n次の球面関数はこれらの線形結合に一意的に表される。帯球関数と縞球関数の全体は球面上で完備直交系をなし、したがって球面上の関数はそれらで直交級数展開される。

［小林良和］

特殊関数と超幾何関数

α、β、γをパラメーターとする関数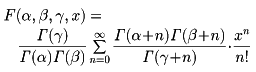

を超幾何関数という。ただし、Γ(z)はガンマ関数である。超幾何関数でパラメーターα、β、γを特殊化することによりいろいろな特殊関数が得られる。たとえば
　　(1+x)^α=F(-α,β,β,-x),
　　P_n(x)=F(-n,n+1,1,(1-x)/2)
である。ただしP_n(x)はルジャンドルの多項式である。超幾何関数はガウスの超幾何方程式
　　x(1-x)y″+(γ-(α+β+1)x)y′-αβy=0
を満たす。α、γをパラメーターとする関数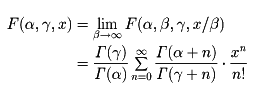

を合流型超幾何関数といい、たとえば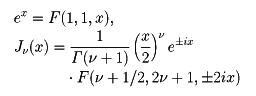

である。ただしJν(x)はベッセル関数である。合流型超幾何関数はクンマーの方程式
　　xy″+(γ-x)y′-αy=0
を満たす。超幾何関数に対し種々の積分表示が知られている。たとえば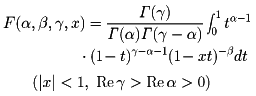

となる。

［小林良和］

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

特殊関数
とくしゅかんすう
special function

初等関数でないもので，理論的にも実用的にも重要な関数には，特殊な名称や記号法が決められており，またグラフや関数表がつくられている。このような関数を総称して特殊関数という。特殊関数でよく知られているものには，ガンマ関数，リーマンのゼータ関数，球関数，円柱関数，楕円関数などがある。その多くは特定の微分方程式の解として導入された。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の特殊関数の言及

【球関数】より

…数理物理学における微分方程式の解として登場する特殊な関数を総称して特殊関数と呼ぶが，なかでも球関数は簡単な式で表され，かつ種々の解析的な特性をもっている重要な例である。それはもっとも基本的な2階微分作用素であるラプラシアンΔに関係する。…

※「特殊関数」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」